Определение 1. Векторы 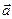 ,
,  ,
,  называются компланарными, если они лежат на одной или параллельных плоскостях.
называются компланарными, если они лежат на одной или параллельных плоскостях.
Определение 2. Базисом в пространстве называется упорядоченная тройка 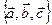 произвольных некомпланарных векторов. АСК в пространстве называется совокупность фиксированной точки
произвольных некомпланарных векторов. АСК в пространстве называется совокупность фиксированной точки 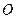 и некоторого базиса
и некоторого базиса 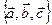 , приведённого к этой точке.
, приведённого к этой точке.
Теорема1. Пусть 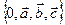 некоторая АСК в пространстве. Тогда любой вектор
некоторая АСК в пространстве. Тогда любой вектор 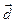 можно представить в виде
можно представить в виде 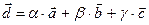 ,
, 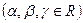 и притом единственным образом.
и притом единственным образом.
Доказательство:
Совместим начало вектора 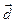 с началом координат точкой
с началом координат точкой 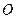 . Проведем через конец вектора
. Проведем через конец вектора 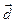 две прямые:
две прямые:
§ первую параллельно вектору  до пересечения с плоскостью, в которой лежат
до пересечения с плоскостью, в которой лежат 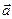 и
и  ;
;
§ вторую параллельно плоскости, в которой лежат 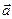 и
и  , до пересечения с прямой, на которой лежит вектор
, до пересечения с прямой, на которой лежит вектор  .
.
Тогда 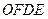 – параллелограмм, следовательно,
– параллелограмм, следовательно, 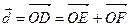 . Вектор
. Вектор 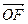 лежит на плоскости, образованной векторами
лежит на плоскости, образованной векторами 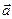 и
и  . По теореме о разложении по базису на плоскости имеем
. По теореме о разложении по базису на плоскости имеем 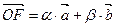 .
.
Вектор 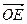 коллинеарен вектору
коллинеарен вектору  , следовательно,
, следовательно, 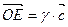 . Таким образом
. Таким образом 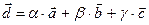 .
.
Нетрудно показать единственность разложения. ■
Пример. Дано: Векторы 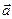 ,
,  и
и  некомпланарны.
некомпланарны.
Доказать: 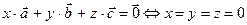 .
.
Доказательство:
Если хотя бы одно из чисел в равенстве, например 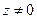 , то равенство
, то равенство 
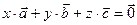 эквивалентно равенству
эквивалентно равенству 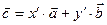 , где
, где 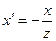 ,
, 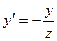 , что означает компланарность векторов
, что означает компланарность векторов 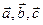 . Получили противоречие условию. Следовательно,
. Получили противоречие условию. Следовательно, 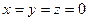 .
.
Обратно: если 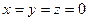 , то равенство
, то равенство 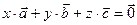 очевидно. ■
очевидно. ■
 2015-06-28
2015-06-28 402
402








