Операции над множествами

Множество, состоящее из элементов, входящих хотя бы в одно из множеств А или В, называются объединением множеств А и В и обозначается АÈ В.

Множество, состоящее из элементов, входящих в оба множества А и В, называются пересечением множеств А и В и обозначается А Ç В.

Множество, состоящее из элементов, входящих в А, но не входящих в В, называется разностью множеств А и В и обозначается А\В.

Если имеется некоторое универсальное множеств V такое, что все рассматриваемые множества являются его подмножествами, то может быть введена операция дополнения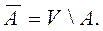

Операции над множествами могут быть наглядно представлены с помощью диаграмм Эйлера-Венна:

	V ФА		V

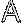
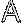
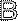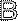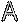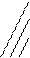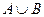
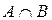
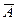
1.3. Свойства операций

Операции 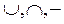производимые над подмножествами некоторого множества V, обладают следующими свойствами:

1. A ÈA=A, AÇA=A -идемпотентность

2. AÈB=BÈA, AÇB=BÇA -коммутативность

3. (A È B) ÈC=AÈ (BÈ C),

(AÇB) ÇC=AÇ(BÇC) -ассоциативность

4. AÈ(AÇB)=A, AÇ (AÈB)=A -поглощение

5. AÇ(BÈC)=(AÇB)È(AÇC),

AÈ(BÇC)=(AÈB) Ç (AÈC) -дистрибутивность

6. AÇ 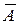= Æ, AÇ Æ=Æ AÈ Æ =A -закон нуля

7. AÈ 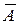=V, AÈV=V, AÇV=A -закон единицы

8. 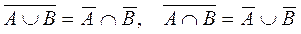-правило де Моргана

9. 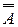=A -инволютивность.

Заметим, что система свойств не изменяется, если одновременно поменять местами операции È и Ç и множества Æ и V. Это есть проявление так называемого принципа двойственности.

Любая структура с 3 операциями, обладающими перечисленными свойствами, называется булевой алгеброй. Множество подмножеств множества V с операциями 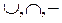образует, следовательно, булеву алгебру.

Отметим, что, если 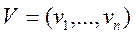- конечное n – элементное множество, то любое его подмножество 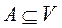может быть задано с помощью двоичного набора .

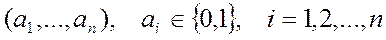При этом 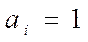означает, что 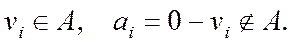Набор 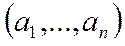называется характеристическим вектором множества А.