Мощность множества.

Мощность конечного множества – это число его элементов, обозначается 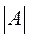. Если 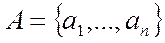, то 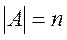. Бесконечные множества считаются равномощными, если между их элементами может быть установлено взаимно однозначное соответствие. Определенная таким образом мощность называется также кардинальным числом. Если элементы множества могут быть поставлены во взаимно однозначное соответствие с членами натурального ряда, то говорят, что оно счетно. Множество рациональных чисел счетно.

Для бесконечных множеств мощности множества и его собственного подмножества могут совпадать, что в определенной степени нарушает привычные представления. Так множество натуральных чисел {1,2,3,...} и множество квадратов натуральных чисел {1,4,9,...} имеют одинаковую мощность. Оба они счетны, что доказывается установлением между их элементами взаимно однозначного соответствия по правилу 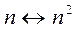, но второе из множеств является подмножеством первого.

Множество действительных чисел не может быть поставлено во взаимно однозначное соответствие с натуральным рядом, поэтому оно имеет большую мощность, которая называется континуум. Множество действительных чисел, принадлежащих отрезку [a;b] или интервалу (a;b) при a<b также имеет мощность континуум.

Докажем, что множество действительных чисел из интервала (0;1) не является счетным, с помощью диагонального метода Кантора. Допустим противное, что это множество счетное. Тогда все числа из (0;1) могут быть выписаны в виде последовательности 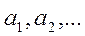. Каждое из этих чисел можно представить в виде бесконечной десятичной дроби

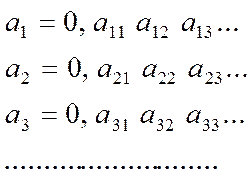
Выпишем теперь число 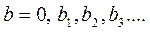, руководствуясь следующим правилом: b₁ - любая десятичная цифра, не равная a₁₁; b₂ - любая цифра, не равная a₂₂; b₃ - не равная a₃₃ и т.д. Тогда 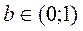, но числа b нет в выписанной последовательности. Полученное противоречие и доказывает несчетность множества действительных чисел из интервала (0;1)