Прямое произведение множеств

Прямым (или декартовым) произведением множеств А и В называется множество 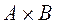, состоящее из всех упорядоченных пар (a,b) таких, что 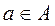и .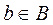

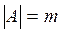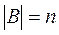Если А и В - конечное множество, мощности и , то .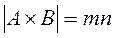

Геометрическим образом множества действительных чисел R является прямая, а геометрическим образом декартового квадрата 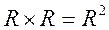является плоскость.

Множество всех двоичных наборов длины n можно рассматривать как 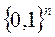- n -ую декартову степень двухэлементного множества 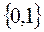. Отсюда следует, что число двоичных наборов длины n равно 2ⁿ. Считая каждый двоичный набор характеристическим вектором подмножества n -элементного множества, получаем, что число всех подмножеств n -элементного множества равно 2ⁿ. Этим объясняется часто используемое обозначение 2^A для множества всех подмножеств A, которое используется как для конечных, так и для бесконечных множеств.

Если A конечное непустое множеств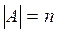о, , то 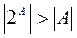, так как 2ⁿ>n при 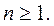Покажем, что для бесконечных множеств данное соотношение между мощностями сохраняется. Допустим противное, пусть между A и 2^A установлено взаимно однозначное соответствие 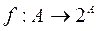. Определим множество 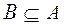следующим образом. Для каждого 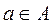включим a в B в том и только в том случае, если 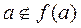. Пусть 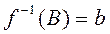, где b -элементы множества A, для которого 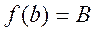. Зададимся теперь вопросом, является ли b элементом множества B? Если 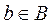, то 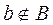по построению множества B. А если 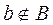, то 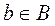опять таки по построению множества B. Таким образом, одновременно имеет место 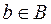и 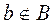. Полученное противоречие и доказывает невозможность установления взаимно однозначного соответствия между A и 2^A.