2015-06-28
843
1*. Используя методы теории множеств, решить задачу:
В результате опроса 76 школьников выяснилось, что 45 занимаются в кружке по рисованию, 31 - в танцевальном кружке, 52 – в кружке «Умелые руки». Три кружка посещают 8 школьников; кружки по рисованию и «Умелые руки» - 28; кружки по рисованию и танцевальный – 16; танцевальный кружок и кружок «Умелые руки» - 20. сколько школьников из опрошенных не занимаются ни в одном кружке?
Решение.
Пусть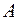 
- множество тех школьников, из 76 опрошенных, которые занимаются в кружке по рисованию, 
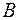- в танцевальном кружке, С – в кружке «Умелые руки». Все эти множества являются подмножествами множества 
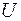всех опрошенных школьников. По условию задачи, 
, 
, 
, 
.
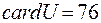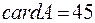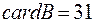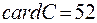Так как школьник, посещающий кружки по рисованию и «Умелые руки», принадлежит и множеству 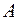, и множеству 
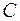, то, следовательно, он принадлежит и множеству 
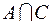. Согласно условию задачи, 
.
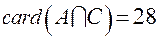Так как школьник, посещающий кружки по рисованию и танцевальный, принадлежит и множеству 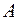, и множеству 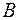, то, следовательно, он принадлежит и множеству 
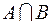. Согласно условию задачи, 
.
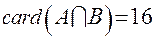Так как школьник, посещающий кружки танцевальный и «Умелые руки», принадлежит и множеству 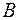, и множеству 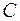, то, следовательно, он принадлежит и множеству 
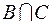. Согласно условию задачи, 
.
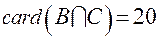Так как школьник, посещающий все кружки принадлежит и множеству 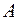, и множеству 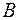, и множеству 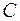, то, следовательно, он принадлежит и множеству 
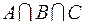. Согласно условию задачи, 
.
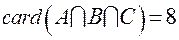Пусть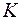 
- множество школьников, занимающихся хотя бы в одном кружке. Тогда 
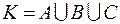. Существует формула:
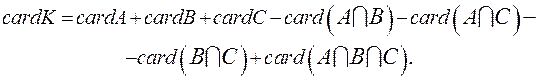
Таким образом,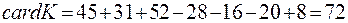 
. Итак, 72 школьника занимаются в каком-либо кружке. Поэтому не занимаются ни в одном кружке 76–72=4 школьника.
Ответ: 4 школьника.
6. «Отношения на множестве»
