Пример 2. 11. Входить в один и тот же класс данного разбиения

а) Отношение равенства 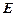на любом множестве является отношением эквивалентности.

Равенство – это минимальное отношение эквивалентности в том смысле, что при удаление любой пары из 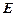(то есть любой единицы на диагонали матрицы 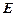) оно перестает быть рефлексивным и, следовательно, уже не является эквивалентностью.

б) Утверждения вида 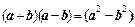или 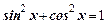, состоящие из формул, соединенных знаком равенства, задают бинарное отношение на множестве формул, описывающих суперпозиции элементарных функций. Это отношение обычно называется отношением равносильности и определяется следующим образом: формулы равносильны, если они задают одну и ту же функцию. Равносильность, хотя и обозначается знаком =, отличается от отношения равенства 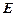, так как оно может выполняться для различных формул. Отношение 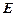для формул – это совпадение формул по написанию. Оно называется графическим равенством.

в) Рассмотрим множество треугольников на плоскости, считая, что треугольник задан, если заданы координаты его вершин. Два треугольника называются конгруэнтными (равными), если они при наложении совпадают, то есть могут быть переведены друг в друга путем некоторого перемещения. Конгруэнтность является отношением эквивалентности на множестве треугольников.

г) Отношение «иметь один и тот же остаток от деления на 9» является эквивалентностью на 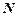. Это отношение выполняется для пар (12, 21), (17, 36) и не выполняется для пар (11, 13), (19, 29).

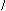Пусть на множестве 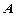задано отношение эквивалентности 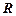. Осуществим следующее построение. Выберем элемент 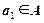и образуем класс (подмножество 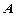) 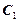, состоящий из 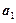и всех элементов, эквивалентных 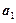; затем выберем элемент 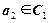и образуем класс 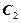, состоящий из 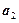и всех элементов, эквивалентных 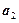, и т.д. Получится система классов 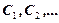(возможно, бесконечная) такая, что любой элемент из 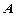входит хотя бы в один класс, то есть 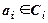. Эта система классов обладает следующими свойствами:

1) она образует разбиение, то есть классы попарно не пересекаются;

2) любые два элемента из одного класса эквивалентны;

3) любые два элемента из разных классов неэквивалентны.

Все эти свойства вытекают из рефлексивности, симметричности и транзитивности 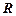. Действительно, если бы классы, например 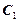и 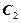, пересекались, то они имели бы общий элемент 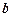, эквивалентны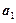й и 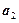, но тогда из-за транзитивности 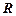было бы 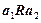, что противоречит построению 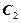. Аналогично доказываются другие два свойства.

Построенное разбиение, то есть система классов, называется системой классов эквивалентности по отношению 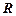. Мощность этой системы называется индексом разбиения. С другой стороны, любое разбиение 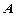на классы определяет некоторое отношение эквивалентности, а именно, отношение «входить в один и тот же класс данного разбиения».