2015-06-28
860
а) Отношения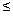 
и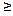 
для чисел являются отношениями нестрого порядка, отношения < и > – отношениями строгого порядка. Оба отношения линейно упорядочивают множества 
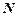и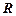 
.
б) Определим отношения 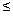и < на 
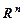следующим образом: 
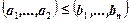, если 
; 
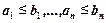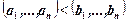, если 
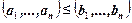и хотя бы в одной координате 
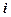выполнено отношение 
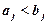. Эти отношения определяют частичный порядок на 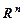: (5, 1/2, -3) < (5, 2/3, -3); (5, 1/2, -3) и (5, 0, 0) не сравнимы.
в) На системе подмножеств множества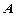 
отношение нестрогого включения 
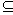задает нестрогий частичный порядок, а отношение строго включения 
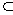задает строгий частичный порядок. Например, 
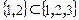сравнимы, а 
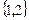и 
не сравнимы, так как элемент 2 не включен во второе множество.
г) Отношения подчиненности на предприятии задает строгий частичный порядок. В нем несравнимыми являются сотрудники разных отделов.
д) Пусть в списке букв конечного алфавита 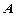порядок букв зафиксирован, то есть всегда один и тот же, как, например, в русском или латинском алфавите. Тогда этот список определяет линейное упорядочение букв, которое назовем отношением предшествования и обозначим 
(
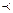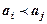, если 
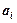предшествует 
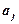в списке букв). На основе отношения предшествования букв строится отношение предшествования слов, определяемое следующим образом. Пусть даны слова 
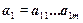и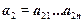 
. Тогда 
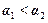, если и только если либо
1) 
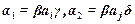и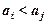 
(
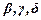– некоторые слова, возможно, пустые, 
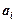и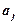 
– буквы), либо
2) 
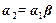, где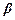 
– непустое слово. Это отношение задает упорядочение множества всех конечных слов в алфавите 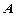, которое называется лексикографическим упорядочением слов.
