1. На числовом примере доказать выражения
1. 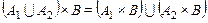 ;
;
2. 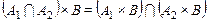 ;
;
3. 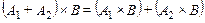 .
.
2. Проверить справедливость нижеследующих равенств для множеств 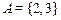 ;
; 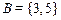 ;
;  и выяснить верны ли равенства для произвольных
и выяснить верны ли равенства для произвольных 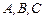 .
.
1. 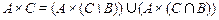 ;
;
2. 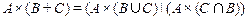 ;
;
3. 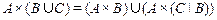 ;
;
4. 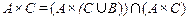 ;
;
5. 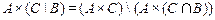 ;
;
6. 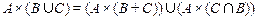 ;
;
7. 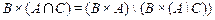 ;
;
8. 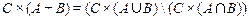 ;
;
9. 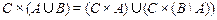 .
.
10. 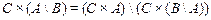 .
.
Пример решения задания 2
Вариант 1
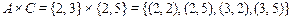 ;
;
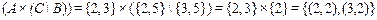 ;
;
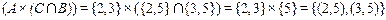 ;
;
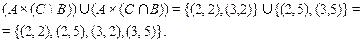
Как видим, равенство для заданных множеств выполняется.
Теперь проверим это равенство для общего случая (произвольных множеств 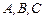 .
.
Пусть 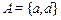 ,
, 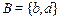 ,
, 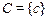 , где
, где 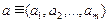 ,
, 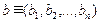 ,
, 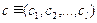 ,
, 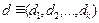 – списки элементов.
– списки элементов.
Тогда 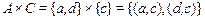 , где
, где 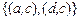 – множества пар элементов, первая компонента которых входит в список
– множества пар элементов, первая компонента которых входит в список 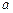 и
и 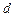 , а вторая – в список
, а вторая – в список 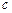 .
.
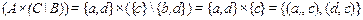 ,
,
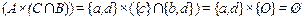 ,
,
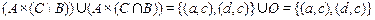 .
.
Как видим множества 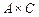 и
и 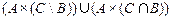 состоят из пар одинакового вида
состоят из пар одинакового вида 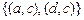 , следовательно, равенство
, следовательно, равенство 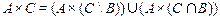 выполняется для произвольных множеств
выполняется для произвольных множеств 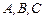 .
.
3. Сравнить кортежи:
1. а) 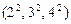 и
и 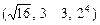 ; б)
; б) 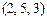 и
и 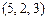 ;
;
в) 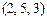 и
и 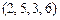 ;
;
2. 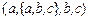 и
и 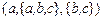 ;
;
3. 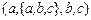 и
и 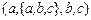 ;
;
4. 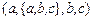 и
и 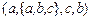 ;
;
5. 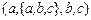 и
и 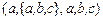
Пример решения задания 3
Вариант 1
а) Кортежи 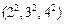 и
и 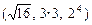 равны, так как
равны, так как 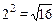 ;
; 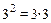 ;
; 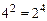 ; б) кортежи
; б) кортежи 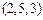 и
и 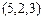 различны, хотя имеют одинаковую длину и одно и то же множество координат, но эти координаты располагаются в разном порядке; в) кортежи
различны, хотя имеют одинаковую длину и одно и то же множество координат, но эти координаты располагаются в разном порядке; в) кортежи 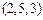 и
и 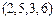 различны, так как имеют разную длину.
различны, так как имеют разную длину.
4. Дано соответствие 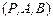 (табл. 2.1).
(табл. 2.1).
1. Изобразить соответствие 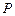 в виде векторной диаграммы.
в виде векторной диаграммы.
2. Выяснить, какими из 4 основных свойств (всюду определенность, сюръективность, функциональность, инъективность) обладает соответствие.
3. Найти образ множества 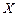 и прообраз множества
и прообраз множества 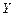 при данном соответствии.
при данном соответствии.
4. Построить соответствие между бесконечными множествами, обладающее тем же набором свойств, что и 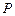 .
.
5. Построить соответствие между конечными множествами, обладающее набором свойств, противоположным данному.
Для данного и построенных соответствий отметить случаи отображений, указать их тип, отметить случаи биекций.
Пример решения задания 4
Вариант 30
1. Изображаем соответствие 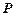 в виде векторной диаграммы (рис. 2.6).
в виде векторной диаграммы (рис. 2.6).
2. Определяем какими из 4 основных свойств обладает данное соответствие.

Таблица 2.1
Варианты задания 4
| Вариант | 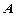 | 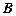 | 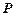 | 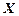 | 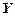 |
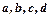 | 1,2,3,4,5 | 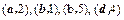 | 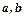 | 3,4 | |
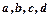 | 1,2,3 | 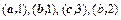 | 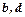 | 1,3 | |
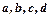 | 1,2,3,4 | 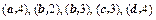 | 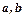 | 3,4 | |
 | 1,2,3,4,5 |  |  | 2,3 | |
 | 1,2,3,4,5 |  |  | 2,3 | |
 | 1,2,3,4,5 |  |  | 2,3 | |
 | 1,2,3,4,5 |  |  | 2,3 | |
 | 1,2,3,4,5 |  |  | 2,3 | |
 | 1,2,3,4,5 |  |  | 2,3 | |
 | 1,2,3,4,5 |  |  | 2,3 | |
 | 1,2,3,4,5 |  |  | 2,3 | |
 | 1,2,3,4,5 |  |  | 2,3 | |
 | 1,2,3,4,5 |  |  | 2,3 | |
 | 1,2,3,4,5 |  |  | 2,3 | |
 | 1,2,3,4,5 |  |  | 2,3 | |
 | 1,2,3,4,5 |  |  | 2,3 | |
 | 1,2,3,4,5 |  |  | 2,3 | |
 | 1,2,3,4,5 |  |  | 2,3 | |
 | 1,2,3,4,5 |  |  | 2,3 | |
 | 1,2,3,4,5 |  |  | 2,3 | |
 | 1,2,3,4,5 |  |  | 2,3 | |
 | 1,2,3,4,5 |  |  | 2,3 | |
 | 1,2,3,4,5 |  |  | 2,3 | |
 | 1,2,3,4,5 |  |  | 2,3 | |
 | 1,2,3,4,5 |  |  | 2,3 | |
 | 1,2,3,4,5 |  |  | 2,3 | |
 | 1,2,3,4,5 |  |  | 2,3 | |
 | 1,2,3,4,5 |  |  | 2,3 | |
 | 1,2,3,4,5 |  |  | 2,3 | |
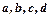 | 1,2,3,4,5 | 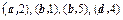 | 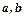 | 3,4 |
а) всюду определенность: для этого необходимо выполнение равенства 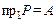 . В примере соответствие
. В примере соответствие 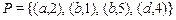 , откуда следует, что проекция соответствия на первую ось равна
, откуда следует, что проекция соответствия на первую ось равна 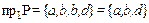 (первые компоненты соответствия
(первые компоненты соответствия 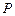 ). При этом исходное множество
). При этом исходное множество 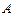 в соответствии
в соответствии 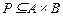 равно
равно 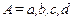 , следовательно
, следовательно 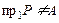 . Таким образом, соответствие не всюду определено.
. Таким образом, соответствие не всюду определено.
б) сюръективность: для этого необходимо выполнение равенства 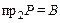 . В примере
. В примере 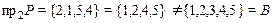 . Соответствие не сюръективно.
. Соответствие не сюръективно.
в) функциональность: для этого необходимо чтобы образом любого элемента из множества 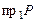 являлся единственный элемент из множества
являлся единственный элемент из множества 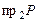 . Сравнивая множества
. Сравнивая множества 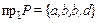 и
и 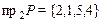 , видим, что одинаковым первым элементам (координатам)
, видим, что одинаковым первым элементам (координатам) 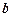 из множества
из множества 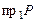 соответствует не единственный элемент из множества
соответствует не единственный элемент из множества 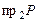 : элементы 1 и 5(соответствие содержит две пары
: элементы 1 и 5(соответствие содержит две пары 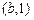 и
и 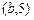 с одинаковыми первыми и различными вторыми координатами). Следовательно, соответствие
с одинаковыми первыми и различными вторыми координатами). Следовательно, соответствие 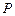 не функционально.
не функционально.
г) инъективность: для этого необходимо чтобы прообразом любого элемента из множества 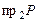 являлся единственный элемент из множества
являлся единственный элемент из множества 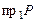 (соответствие не должно содержать пар с одинаковыми вторыми и различными первыми координатами). Пар с одинаковыми вторыми и различными первыми координатами в данном соответствии не имеется, следовательно, оно инъективно.
(соответствие не должно содержать пар с одинаковыми вторыми и различными первыми координатами). Пар с одинаковыми вторыми и различными первыми координатами в данном соответствии не имеется, следовательно, оно инъективно.
3. Найдем образ 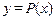 и прообраз
и прообраз 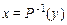 при соответствии
при соответствии 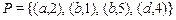 .
.
Так как 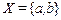 , а элементы
, а элементы 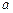 и
и 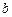 образуют в исходном соответствии подмножество
образуют в исходном соответствии подмножество 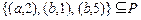 , то образ
, то образ 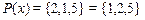 .
.
Так как 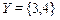 , а один элемент 4 образует в исходном соответствии подмножество
, а один элемент 4 образует в исходном соответствии подмножество 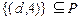 , то прообраз
, то прообраз 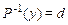 .
.
4. Построим соответствие между бесконечными множествами, обладающее тем же набором свойств, что и 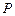 .
.
Пусть 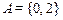 ,
, 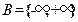 ,
, 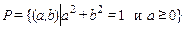 .
.
Графиком данного соответствия будет полукруг (рис. 2.7), из которого видно, что 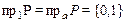 ,
, 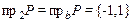 , а само соответствие в виде множества
, а само соответствие в виде множества 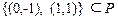 .
.
а) Построенное соответствие не всюду определено, так как 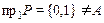 .
.
б) Построенное соответствие не сюръективно, так как 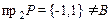 .
.

а) Построенное соответствие не всюду определено, так как 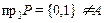 .
.
б) Построенное соответствие не сюръективно, так как 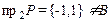 .
.
в) Построенное соответствие не функционально, так как содержит пары с одинаковыми первыми и различными вторыми координатами, например, 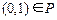 и
и 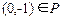 .
.
г) Соответствие инъективно, так как не содержит пар с различными первыми и одинаковыми вторыми координатами.
5. Построим соответствие между конечными множествами, обладающее набором свойств, противоположным исходному, то есть такое, чтобы оно было всюду определено, сюръективно, функционально, не инъективно.
Пусть 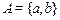 ,
, 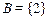 ,
, 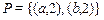 . Векторная диаграмма данного соответствия представлена на рис. 2.8.
. Векторная диаграмма данного соответствия представлена на рис. 2.8.
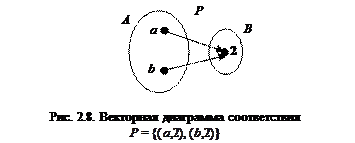
а) Данное соответствие всюду определено, так как 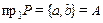 .
.
б) Соответствие сюръективно, так как 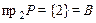 .
.
в) Соответствие функционально, так как оно не содержит пар с одинаковыми первыми и различными вторыми координатами.
г) Соответствие не инъективно, так как содержит две пары 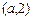 и
и 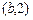 с одинаковыми вторыми и различными первыми координатами.
с одинаковыми вторыми и различными первыми координатами.
Так как построенное соответствие всюду определено, сюръективно и функционально, то оно является отображением 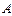 на
на 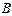 .
.
5. Дано отношение 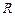 , заданное на множестве
, заданное на множестве 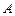 (табл. 2.2).
(табл. 2.2).
1. Выяснить, какими из свойств: рефлексивность, антирефлексивность, симметричность, антисимметричность, транзитивность, связность обладает отношение 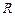 , заданное на множестве
, заданное на множестве 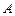 .
.
2. Построить на конечном множестве отношение, обладающее таким же набором свойств, что и данное.
3. Построить на бесконечном множестве отношение, обладающее набором свойств, противоположным данному. В случае невозможности построения доказать противоречивость набора требований.
Пример решения задания 5
Вариант 9
1. Выясним, какими свойствами обладает данное отношение.
Таблица 2.2
Варианты задания 4
| Вариант | 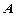 | 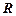 |
| Множество студентов ВУЗа | 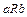 , , 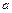 и и 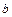 учатся на одном факультете учатся на одном факультете | |
| Множество окружностей на плоскости | 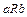 , , 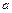 касается касается 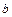 | |
| Жители страны на начало этого года | 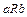 , , 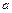 и и 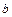 – супруги – супруги | |
| Жители страны на начало этого года | 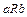 , , 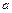 и и 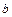 состоят в одной и той же политической партии состоят в одной и той же политической партии | |
| Прямые в пространстве | 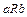 , , 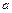 и и 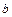 имеют хотя бы одну общую точку имеют хотя бы одну общую точку | |
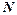 | 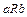 , , 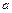 и и 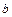 имеют одинаковый остаток от деления на 5 имеют одинаковый остаток от деления на 5 | |
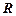 | 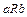 , , 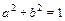 | |
| Читатели библиотеки вашего ВУЗа | 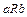 , , 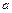 и и 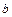 прочитали одну и ту же книгу прочитали одну и ту же книгу | |
| Множество теннисистов турнира, в котором каждый должен сыграть 3 партии | 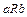 , , 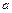 обыграл обыграл 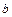 порезультатам личных встреч порезультатам личных встреч |
1) Отношение 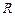 не является рефлексивным, так как не может обыграть сам себя.
не является рефлексивным, так как не может обыграть сам себя.
2) Отношение 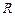 является антирефлексивным, так как каждый теннисист не обыграл сам себя (не выполняется рефлексивность).
является антирефлексивным, так как каждый теннисист не обыграл сам себя (не выполняется рефлексивность).
3) Отношение 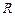 не является симметричным, так как найдется пара теннисистов
не является симметричным, так как найдется пара теннисистов 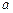 и
и 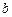 такая, что
такая, что 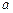 обыграл
обыграл 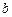 по очкам в личных встречах, а
по очкам в личных встречах, а 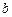 не обыграл
не обыграл 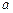 .
.
4) Отношение 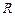 является антисимметричным, так как если
является антисимметричным, так как если 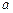 обыграл
обыграл 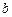 , то
, то 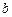 обязательно не обыграл
обязательно не обыграл 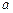 (не выполняется симметричность).
(не выполняется симметричность).
5) Отношение 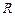 не является транзитивным, так как может сложиться ситуация, когда
не является транзитивным, так как может сложиться ситуация, когда 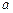 обыграл
обыграл 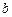 ,
, 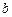 обыграл
обыграл 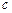 , и в то же время
, и в то же время 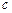 обыграл
обыграл 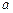 .
.
6) Отношение 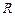 является связным, так как любая пара спортсменов должна сыграть между собой и выявить победителя.
является связным, так как любая пара спортсменов должна сыграть между собой и выявить победителя.
2. Построим на конечном множестве отношение, обладающее
таким же набором свойств, что и данное.
Пусть конечное множество равно 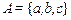 , а отношение
, а отношение 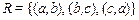 . Изобразим это отношение в виде графа (рис. 2. 8).
. Изобразим это отношение в виде графа (рис. 2. 8).
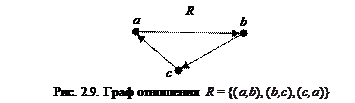
1) Это отношение не является рефлексивным, так как 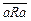 .
.
2) Отношение антирефлексивно, так как 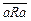 ,
, 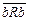 ,
, 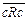 .
.
3) Отношение не симметрично, так как 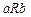 и
и 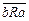 .
.
4) Отношение антисимметрично, так как 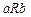 и
и 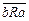 ,
, 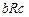 и
и 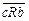 ,
, 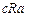 и
и 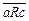 .
.
5) Отношение не транзитивно, так как 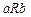 и
и 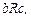 но
но 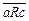 .
.
6) Отношение связно, так как любая пара различных элементов из множества 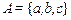 вступает в отношение
вступает в отношение 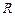 в том или ином порядке.
в том или ином порядке.
3. Построим на бесконечном множестве отношение, обладающее набором свойств, противоположным исходному, то есть рефлексивное и не антирефлексивное, симметричное и не антисимметричное, транзитивное и не связное.
Пусть 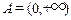 , и отношение
, и отношение 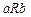 означает, что
означает, что 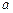 и
и 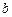 имеют одинаковую дробную часть. Тогда это отношение будет обладать следующими свойствами.
имеют одинаковую дробную часть. Тогда это отношение будет обладать следующими свойствами.
1. Отношение рефлексивно, так как любое число имеет одинаковую дробную часть само с собой.
2. Отношение не антирефлексивно, так как найдется число, например, 2,34, имеющее одинаковую дробную часть само с собой.
3. Отношение симметрично, так как если 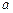 и
и 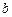 имеют одинаковую дробную часть, то
имеют одинаковую дробную часть, то 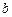 и
и 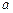 также имеют одинаковую дробную часть.
также имеют одинаковую дробную часть.
4. Отношение 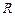 не антисимметрично, так как, например, числа 2,35 и 3,35 не равны, и в то же время они находятся в отношении 2, 35
не антисимметрично, так как, например, числа 2,35 и 3,35 не равны, и в то же время они находятся в отношении 2, 35 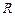 3, 35 и 3,35
3, 35 и 3,35 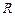 2,35.
2,35.
5. Отношение является транзитивным, так как если 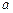 и
и 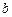 имеют одинаковую дробную часть,
имеют одинаковую дробную часть, 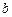 и
и 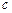 имеют одинаковую дробную часть, то
имеют одинаковую дробную часть, то 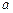 и
и 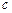 также имеют ту же самую дробную часть.
также имеют ту же самую дробную часть.
6. Отношение не связно, так как, например, числа 3,1 и 1,6 не равны, но 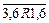 и
и 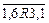 .
.
Это отношение рефлексивно, симметрично и транзитивно, значит, оно является отношение эквивалентности.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Дать определение декартова (прямого) произведения. В каком виде оно задается? Представить его геометрически.
2. Какой закон выполняется для декартова произведения множеств? Записать его.
3. Что такое кортеж и чему равна его длина? Примеры кортежей. Основные отличия понятий кортежа и множества.
4. Что называется степенью декартова произведения? Что представляют собой проекции кортежей на оси, их обозначения, как определяются проекции?
5. Дать определение соответствия между множествами А и В, привести его обозначение. Что предполагает соответствие?
6. Привести графическое изображение соответствия на примерах.
7. Дать определение образа и прообраза элемента, области определения и области значений соответствия, всюду определенного и сюръективного соответствия, инъективного и функционального соответствия.
8. Что такое взаимнооднозначное соответствие, биекция, отображения 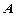 в
в 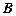 и
и 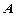 на
на 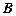 , равномощные, счетные и континуальные множества?
, равномощные, счетные и континуальные множества?
9. Привести геометрическую иллюстрацию и примеры соответствий.
10. Дать определение отношений, как они называются в зависимости от числа связей между ними? Какое отношение называется бинарным? Привести примеры отношений.
11. Как задается с помощью матриц бинарное отношение? Привести примеры.
12. Что понимают под рефлексивным и антирефлексивным отношением, как записываются эти свойства? Примеры.
13. Какие отношения обладают свойством симметричности и антисимметричности, их запись? Примеры.
14. Дать определения транзитивного и связного отношения, их запись и привести примеры.
15. Что такое транзитивное замыкание отношений? Привести его запись.
16. С помощью каких выражений определяются свойства бинарных отношений?
17. Что такое отношения частичного, линейного, строгого и строгого линейного порядка?
18. Какие отношения являются отношениями эквивалентности, их свойства? Что такое фактор-множества, индекс разбиения, примеры отношений эквивалентности.
19. Какие отношения являются отношениями строгого и нестрогого порядка, линейно и частично упорядоченными множествами? Привести примеры.
20. Дать определение функциональных отношений.
 2015-06-28
2015-06-28 2534
2534
