Определение. Векторным произведением вектора  на вектор
на вектор  называется вектор
называется вектор 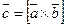 , если:
, если:
1) 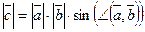 ;
;
2) 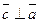 и
и 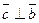 ;
;
3) векторы 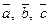 образуют правую тройку.
образуют правую тройку.
Геометрические свойства векторного произведения.
Свойство 1. Необходимым и достаточным условием коллинеарности двух векторов  и
и  является равенство их векторного произведения, т.е.
является равенство их векторного произведения, т.е. 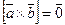 .
.
Доказательство. Необходимость. Пусть 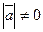 ,
, 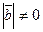 ,
, 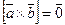 , тогда
, тогда 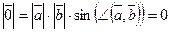 . Следовательно,
. Следовательно, 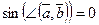 и
и 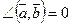 , поэтому
, поэтому 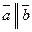 , т.е.
, т.е.  и
и  коллинеарны.
коллинеарны.
Достаточность. Пусть  и
и  коллинеарны, тогда
коллинеарны, тогда 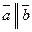 и
и 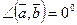 или
или 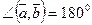 . Поэтому
. Поэтому 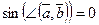 и
и 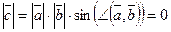 . Так как только нулевой вектор имеет нулевую длину, то
. Так как только нулевой вектор имеет нулевую длину, то 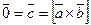 . □
. □
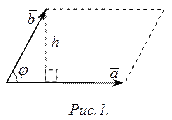
Свойство 2. Абсолютная величина векторного произведения равна площади параллелограмма, образованного этими векторами, т.е. 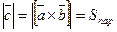 .
.
Доказательство. 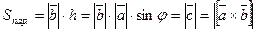 . □
. □
 2015-06-28
2015-06-28 392
392








