Определение 1. Под скалярным произведением двух векторов  и
и  понимается число, равное произведению длин этих векторов на косинус угла между ними, т.е.
понимается число, равное произведению длин этих векторов на косинус угла между ними, т.е.
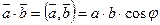 ,
,
где 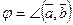 .
.
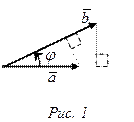
Так как 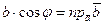 и
и 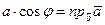 (рис.1), то скалярное произведение можно записать в виде
(рис.1), то скалярное произведение можно записать в виде
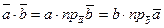 .
.
Определение 2. Два вектора  и
и  называются ортогональными, если угол между ними равен
называются ортогональными, если угол между ними равен 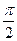 . Ортогональность векторов
. Ортогональность векторов  и
и  обозначается
обозначается 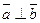 .
.
Теорема (геометрическое свойство скалярного произведения). 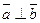 тогда и только тогда, когда
тогда и только тогда, когда 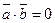 .
.
Доказательство. Необходимость. Пусть 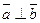 , тогда
, тогда 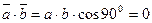 .
.
Достаточность. Если 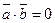 , то
, то 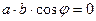 . Возможны три случая:
. Возможны три случая:
1) 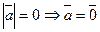 ;
;
2) 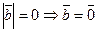 ;
;
3)  .
.
Из этих случаев следует, что 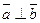 .□
.□
Алгебраические свойства скалярного произведения.
1. 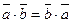 .
.
2. 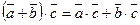 .
.
3. 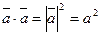 .
.
4. 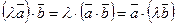 .
.
 2015-06-28
2015-06-28 492
492








