2015-06-28
455
Свойство 1. Если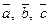 
компланарные, то 
.
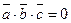Доказательство. Пусть 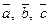компланарные. Запишем смешанное произведение этих векторов:
.
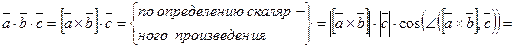
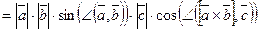Рассмотрим случаи:
1. Если один из векторов нулевой, то .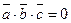
2. Если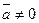 
, 
, 
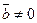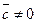и вектора 
и 
‑ коллинеарные, то 
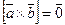и, следовательно, .
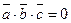3. Пусть 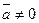, , 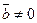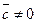и вектора и ‑ неколлинеарные. Тогда из того, что вектор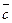 
лежит в одной плоскости с векторами и , а вектор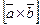 
перпендикулярен этой плоскости, вытекает, что векторы 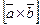и 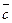‑ перпендикулярные (т.е. 
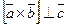), поэтому
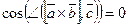и . □
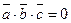Свойство 2. Если 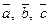некомпланарные, то приведя их к общему началу и построив на них параллепипед объема 
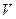, получим 
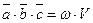, где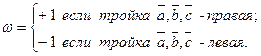 
Доказательство. Из определения и свойств векторного произведения имеем:
,
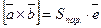где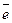 
‑ единичный вектор, такой, что 
, 
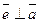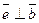и тройк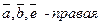а 
, а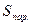 
‑ площадь параллелограмма, построенного на векторах и .
.
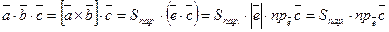Рассмотрим два случая.
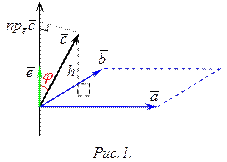
1. Тройка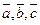 
‑ правая (рис.1), тогда угол 
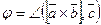‑ острый, т.е. 
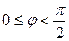, и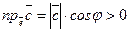 
. Если 
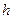‑ высота параллепипеда, построенного на векторах 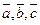, то в этом случае 
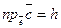и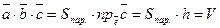 
.
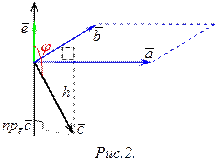
2. Тройка 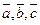‑ левая (рис.2), тогда угол 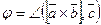‑ тупой, т.е. 
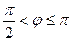, и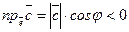 
. В этом случае 
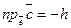и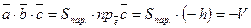 
.
Из рассмотренных случаев следует, что 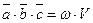, где □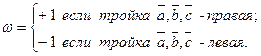
Свойство 3. Смешанное произведение не меняется при циклической перестановке, т.е.
.
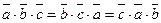Доказательство. Пусть 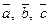‑ некомпланарные.
Докажем, что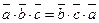 
.
По свойству 2,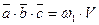 
и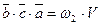 
. Так как циклическая перестановка не меняет ориентацию тройки, то 
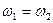и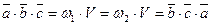 
.
Равенство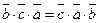 
доказывается аналогично. □
Свойство 4. При перестановке двух соседних множителей, смешанное произведение меняет знак, т.е.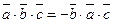 
.
Доказательство. Пусть 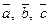‑ некомпланарные. Докажем, что 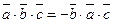. По свойству 2, 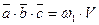и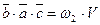 
. Так как нециклическая перестановка меняет ориентацию тройки, то 
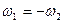и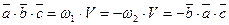 
.□
Свойство 5.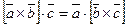 
.
Доказательство. Из свойства скалярного произведения следует, что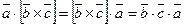 
. Поэтому надо доказать, что 
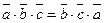. Так как перестановка циклическая, то по свойству 3 это равенство выполняется. □
