2015-06-28
617
Пусть вектор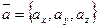 
задан проекциями на оси 
, 
, 
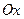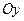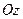. Введём (орты) единичные векторы 
, 
, 
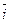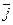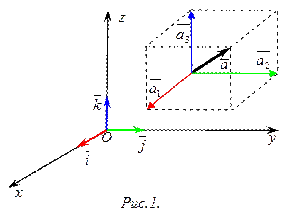
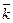, направленные по осям координат, и построим параллепипед (рис.1), диагональю которого является вектор 
, тогда вектора 
, 
, 
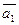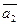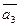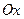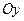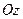будут компонентами вектора относительно осей , , и
, 
, 
.
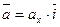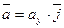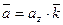Подставим эти выражения в равенство
,
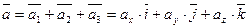в результате получили координатную формулу вектора
.
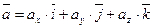Линейные операции над векторами теперь можно записать в координатной форме.
Если 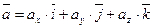и 
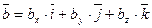, то
1) 
,
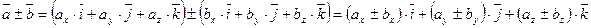т.е.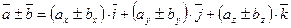 
или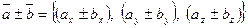 
,
при сложении (или вычитании) векторов их одноименные координаты складываются (вычитаются);
2) 
,
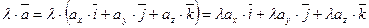т.е.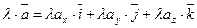 
и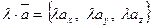 
,
при умножении вектора на скаляр координаты вектора умножаются на этот скаляр.
