2015-06-24
662
Мы дадим определение корреляционных функций, записав их в представлении первичного квантования и выразив через многочастичную волновую функцию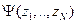 
системы, где 
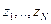- координаты 
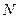частиц. Мы рассмотрим предел нулевой температуры и обозначим волновую функцию основного состояния как 
.
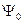Одночастичная матрица плотности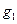 
описывает пространственные корреляции между двумя точками 
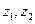. В однородной системе 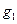зависит только от разности 
:
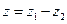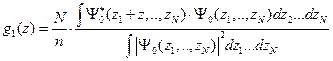
| (4.1) |
где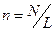 
- погонная плотность.
Функция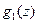 
нормирована таким образом, чтобы ее значение в нуле было единичным 
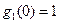. Как мы убедимся позже, на больших расстояниях одночастичная матрица плотности одномерной однородной системы при нулевой температуре затухает полиномиально быстро, что свидетельствует об отсутствии бозе-конденсата в такой системе.
Функция парного распределения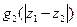 
дает вероятность того, что одна частица будет найдена в положении 
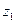в то время как другая находится в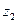 
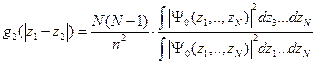
| (4.2) |
На больших расстояниях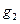 
выходит на 
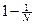и стремится к единичному значению в термодинамическом пределе 
.
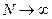Значение в нуле трехчастичной матрицы плотности дает вероятность обнаружить три частицы в одном и том же месте:
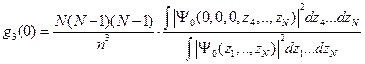
| (4.3) |
Зависимость этой величины от плотности представляет большой практический интерес, т.к. она позволяет предсказать потерю частиц из конденсата за счет трехчастичной рекомбинации.
Фурье-преобразование связывает изложенные функции с не менее интересными функциями. А именно, импульсное распределение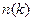 
связано с одночастичной матрицей плотностью (4.1):
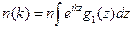
| (4.4) |
а статический структурный фактор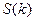 
прямо связан с функцией парного распределения (4.2):
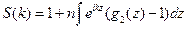
| (4.5) |
Информация об импульсном распределении может быть получена из наблюдения за скоростью расширении конденсата после выключения ловушки. Статический структурный фактор может быть измерен при помощи метода бреговской спектроскопии.
| Энергетический спектр случайных сигналов |
| При спектральных измерениях случайных последовательностей встречается ряд трудностей. Во-первых, обычно интерес представляет энергетический спектр (определение энергетического спектра еще не было дано). Во-вторых, измерения должны быть статистически устойчивыми в том смысле, что, какая бы оценка ни рассматривалась, при увеличении интервала измерения она должна сходиться к вполне конкретной величине. Простое и удобное условие сходимости сводится к тому, чтобы дисперсия оценки стремилась к нулю при увеличении интервала измерения. Известно, что при работе с энергетическим спектром весьма удобно пользоваться корреляционной функцией сигнала. В связи с этим в данном разделе будут кратко рассмотрены понятия корреляционной функции и энергетического спектра и связывающие их соотношения. Затем будут проанализированы с точки зрения эффективности вычислений два хорошо известных метода расчета энергетического спектра случайных сигналов. До сих пор использовалось довольно общее определение спектра. Он определялся как значение z-преобразования в одной или ряде точек в z-плоскости. В связи с этим возникает следующий вопрос: можно ли энергетический спектр сигнала определить >в таком же общем виде? По-видимому, разумным подходом является следующий: если задана спектральная плотность мощности на некоторой кривой в z-плоскости (по обязательно на единичной окружности), |
