ИХ, передаточная функция, частотные характеристики цифровых фильтров и связь между ними

25 26 27 28 29 30 31

Импульсная реакция фильтров.
Функция отклика. Если на вход нерекурсивного фильтра подать единичный импульс (импульс Кронекера), расположенный в точке k = 0, то на выходе фильтра мы получим его реакцию на единичный входной сигнал (формула 2.1.3), которая определяется весовыми коэффициентами b_n оператора фильтра:
y(k) = TL[d(0)] = b_n③ d(k-n) = h(k) º b_n (2.2.1)
Для рекурсивных фильтров реакция на импульс Кронекера зависит как от коэффициентов b_n фильтра, так и от коэффициентов обратной связи a_m. С использованием формулы (2.1.2):
y(k) = 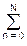b_nd(k-n) – 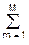a_my(k-m) = h_k. (2.2.1')
Функция h(k), которая связывает вход и выход фильтра по реакции на единичный входной сигнал и однозначно определяется оператором преобразования фильтра, получила название импульсного отклика фильтра (функции отклика).
Если произвольный сигнал на входе фильтра представить в виде линейной комбинации взвешенных импульсов Кронекера
x(k) = 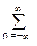d(n) x(k-n),
то, с использованием функции отклика, сигнал на выходе фильтра можно рассматривать как суперпозицию запаздывающих импульсных реакций на входную последовательность взвешенных импульсов:
y(k) = 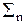h(n) (d(n) x(k-n)) º 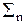h(n) x(k-n).
Для нерекурсивных фильтров пределы суммирования в последнем выражении устанавливаются непосредственно по длине импульсного отклика h(n). Для рекурсивных фильтров длина импульсного отклика, в принципе, может быть бесконечной.
2.3. Передаточные функции фильтров /7/.
Z-преобразование. Удобным методом решения разностных уравнений линейных систем является z-преобразование. Применяя z-преобразование к обеим частям равенства (2.1.1), c учетом сдвига функций (y(k-m) ó z^m Y(z)), получаем:
Y(z) 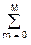a_mz^m = X(z) 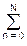b_nzⁿ, (2.3.1)
где X(z),Y(z)- соответствующие z-образы входного и выходного сигнала. Отсюда, полагая a_o = 1, получаем в общей форме функцию связи выхода фильтра с его входом - уравнение передаточной функции системы в z-области:
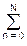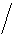H(z) = Y(z)/X(z) = b_nzⁿ (1+ 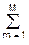a_mz^m). (2.3.2)
Для НЦФ, при нулевых коэффициентах a_m: H(z) = 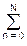b_nzⁿ. (2.3.3)
При проектировании фильтров исходной, как правило, является частотная передаточная функция фильтра H(ω), по которой вычисляется ее Z-образ H(z) и обратным переходом в пространство сигналов определяется алгоритм обработки данных. В общей форме для выходных сигналов фильтра:
Y(z) = H(z)·X(z).
Y(z)·(1+ 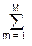a_m z^m) = X(z) 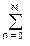b_n zⁿ
Y(z) = X(z) 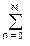b_n zⁿ – Y(z) 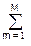a_m z^m. (2.3.4)
После обратного Z-преобразования выражения (2.3.4):
y(k) = 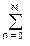b_n x(k-n) – 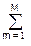a_m y(k-m). (2.3.5)
При подаче на вход фильтра единичного импульса Кронекера _о, имеющего z-образ (z) = zⁿ= 1, сигнал на выходе фильтра будет представлять собой импульсную реакцию фильтра y(k) ≡ h(k), при этом:
H(z) = Y(z)/(z) = Y(z) = TZ[y(k)] = 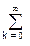h(k) z^k, (2.3.6)
т.е. передаточная функция фильтра является z-образом его импульсной реакции. При обратном z-преобразовании передаточной функции соответственно получаем импульсную характеристику фильтра:
h(k) ó H(z). (2.3.7)
Если функция H(z) представлена конечным степенным полиномом, что, как правило, характерно для НЦФ, являющихся КИХ-фильтрами, то обратное z-преобразование осуществляется элементарно идентификацией коэффициентов по степеням z. Передаточная функция РЦФ также может быть представлена степенным полиномом прямым делением числителя на знаменатель правой части выражения (2.3.2), однако результат при этом может оказаться как конечным, так и бесконечным, т.е. система может иметь либо конечную, либо бесконечную импульсную характеристику. Практически используемые рекурсивные фильтры обычно имеют бесконечную импульсную характеристику (БИХ-фильтры) при конечном числе членов алгоритма фильтрации (2.3.5).
Частотные характеристики фильтров
Общие понятия. От z-образов сигналов и передаточных функций подстановкой z = exp(-jwDt) в уравнение (2.3.2) можно перейти к Фурье-образам функций, т.е. к частотным спектрам сигналов и частотной характеристике фильтров, а точнее – к функциям их спектральных плотностей.
Можно применить и способ получения частотных характеристик непосредственно из разностного уравнения системы обработки данных. Так как цифровая фильтрация относится к числу линейных операций, то, принимая для сигнала на входе фильтра выражение x(kDt) = B(w) exp(jwkDt), мы вправе ожидать на выходе фильтра сигнал y(kDt) = A(w) exp(jwkDt). Подставляя эти выражения в разностное уравнение фильтра (2.1.1), получаем:
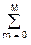a_mA(w) exp(jwkDt-jwmDt) = 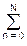b_nB(w) exp(jwkDt-jwnDt).
A(w) exp(jwkDt) 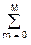a_mexp(-jwmDt) = B(w) exp(jwkDt) 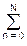b_nexp(-jwnDt).
A(w) 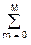a_m exp(-jwmDt) = B(w) 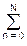b_n exp(-jwnDt). (2.4.1)
Передаточная частотная функция (частотная характеристика при а_о=1):
H(w) = A(w)/B(w) = 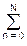b_n exp(-jwnDt) 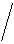[1+ 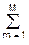a_mexp(-jwmDt)]. (2.4.2)
Нетрудно убедиться, что полученная частотная характеристика повторяет функцию (2.3.2) при z = exp(-jwDt), что и следовало ожидать. Аналогично z-преобразованию (2.3.7), частотная характеристика фильтра представляет собой Фурье-образ его импульсной реакции, и наоборот. При Dt = 1:
H(w) = 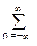h(n) exp(-jwn), (2.4.3)
h(n) = (1/2p) 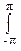H(w) exp(jwn) dw. (2.4.4)
В общем случае H(w) является комплексной функцией, модуль которой R(w) называется амплитудно-частотной характеристикой (АЧХ), а аргумент j(w) – фазово-частотной характеристикой (ФЧХ).
A(w) = |H(w)| =
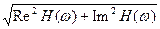
j(w) = arctg(-Im H(w)/Re H(w)).
Выбор знака фазового угла ориентирован на каузальные системы с отрицательным временным запаздыванием сигналов. Допустим, что система осуществляет только сдвиг сигнала x(t) вправо по временной оси, т е. y(t) = x(t-t). Для преобразования Фурье функции y(t) имеем:
Y(f) = 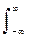y(t) exp(-j2pft) dt = 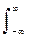x(t-t) exp(-j2pft) dt =
= exp(-j2pft) 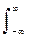x(t) exp(-j2pft) dt = exp(-j2pft) X(f).
Отсюда:
H(f) = Y(f)/X(f) = exp(-j2pft), |H(f)| = 1, j_h(f) = -2pft.
Из последнего равенства следует, что фаза представляет собой прямую с отрицательным тангенсом угла наклона -2pft. Соответственно, для всех каузальных фильтров, осуществляющих преобразование с определенной задержкой сигнала на выходе, при выполнении операции над частотными составляющими сигнала имеет место:
Y(f) = H(f) X(f) = |H(f)| exp(jj_h(f)) |X(f)| exp(jj_x(f)) = |H(f)| |X(f)| exp{j [j_h(f)+j_x(f)]},
|Y(f)| = |H(f)| |X(f)|, j_y(f) = j_h(f)+j_x(f).
C учетом отрицательного знака j_h(f) фазовой характеристики каузальных фильтров это вызывает сдвиг в "минус" всех частотных составляющих сигнала и соответствующую задержку выходного сигнала относительно входного.
На рис. 2.4.1-2.4.3 приведены частотные характеристики фильтров (модули и аргументы спектральных плотностей), которые были рассмотрены выше в примерах и на рис. 2.1.4 – 2.1.6. Графики приведены в границах главных диапазонов спектров, и получены непосредственной подстановкой z=exp(-jwDt) при Dt=1 в уравнения передаточных функций H(z).
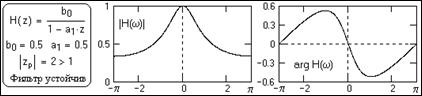
Рис. 2.4.1. Спектр не имеет особых точек.
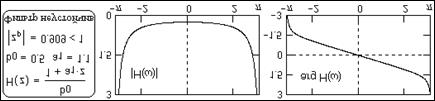
Рис. 2.4.2. Спектр имеет особые точки на границах диапазонов.
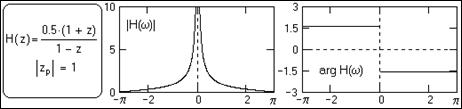
Рис. 2.4.3. Спектр интегрирующего фильтра. Особая точка на нулевой частоте.
При обработке ограниченных массивов амплитуда центрального пика равна количеству точек массива.
Основные свойства частотных характеристик цифровых фильтров:
1. Частотные характеристики являются непрерывными функциями частоты.
2. При дискретизации данных по интервалам Dt функция H(w) является периодической. Период функции H(w) равен частоте дискретизации входных данных F = 1/Dt. Первый низкочастотный период (по аргументу w от -p/Dt до p/Dt, по f от -1/2Dt до 1/2Dt) называется главным частотным диапазоном. Граничные частоты главного частотного диапазона соответствуют частоте Найквиста ±w_N, w_N= p/Dt. Частота Найквиста определяет предельную частоту данных, которую способен обрабатывать фильтр.
3. Для фильтров с вещественными коэффициентами импульсной реакции h(nDt) функция АЧХ является четной, а функция ФЧХ - нечетной. С учетом этого частотные характеристики фильтров обычно задаются только на интервале положительных частот 0-w_N главного частотного диапазона. Значения функций на интервале отрицательных частот являются комплексно сопряженными со значениями на интервале положительных частот.
Как правило, при частотном анализе фильтров значение Dt интервала дискретизации принимают за 1, что соответственно определяет задание частотных характеристик на интервале (0,p) по частоте w или (0,1/2) по f. При использовании быстрых преобразований Фурье (БПФ) вычисления спектров осуществляются в одностороннем варианте положительных частот в частотном интервале от 0 до 2p (от 0 до 1 Гц), где комплексно сопряженная часть спектра главного диапазона (от -p до 0) занимает интервал от p до 2p (для ускорения вычислений используется принцип периодичности дискретных спектров). Заметим, что при выполнении БПФ количество точек спектра равно количеству точек входной функции, а, следовательно, отсчет на частоте 2p, комплексно сопряженный с отсчетом на частоте 0, отсутствует. При нумерации точек входной функции от 0 до N он принадлежит точке N+1 - начальной точке следующего периода, при этом шаг по частоте равен 2p/(N+1). Современное программное обеспечение БПФ допускает любое количество точек входной функции, при этом для нечетного значения N частоте p соответствует отсчет на точке (N+1)/2, не имеющий сопряженного отсчета, а при четном значении N отсутствует отчет на частоте p (она располагается между отсчетами k=N/2 и N/2 +1). Отсчетам с номерами k главного диапазона БПФ (за исключением точки k=0) соответствуют комплексно сопряженные отсчеты N+1-k (за исключением точки k=(N+1)/2 при нечетном N).