2015-06-24
455
1. Z- преобразование и его свойства.
Удобным способом анализа дискретных последовательностей является z-преобразования. Смысл его заключается в том, что последовальности чисел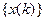 
ставится в соответствие функция комплексной переменной z, определяемая следующим образом: 
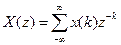. Разумеется, функция 
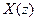определена только для тех значений z, при которых ряд сходится.
Z-преобразования играет для дискретных сигналов и систем такую же роль, как преобразование Лапласа – для аналоговых.
Свойства z-преобразования:
1. Линейность. Если последовательност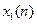и 
и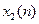 
имеют z-образы 
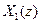и 
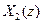, то z-образ их линейной комбинации будет 
.
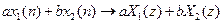2. 
Задержки или смещение. Если z-образ последовательности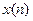 
равен 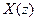, то z-образ последовательности с задержкой m элементов будет 
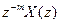. Это свойство широко используется для превращения передаточной функции z систем дискретного времени в разностные уравнения во временной области, и наоборот: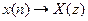 
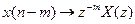
3. Свертка. Задаем выход системы: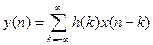 
. Выраженные через z-образы вход и выход связаны: 
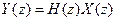, где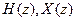 
, 
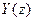- соответственно z-образы последовательносте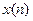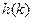й , 
и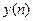 
. При заданных 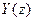выход 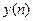можно найти с помощью обратного z-преобразования .
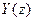4. Дифференцирование. Если 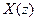- z-образ последовательности 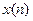, то z-образ 
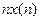можно найти, продифференцировав : , 
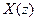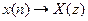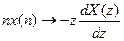. Полезно использовать, когда 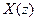содержит полюсы высокого порядка.
5. Взаимосвязь с преобразованием Лапласа. Системы или сигналы непрерывного времени описываются с помощью преобразования Лапласа. Если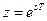 
, где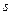 
- комплексная переменная Лапласа, которая задается как: 
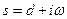, то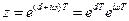 
. Следовательно 
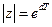и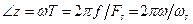 
, 
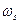- частота дискретизации.
