Эти понятия относятся к числу базовых в теории погрешностей.
Обозначим через 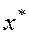 точное значение некоторой величины, через x,- его приближенное значение. Тогда разность
точное значение некоторой величины, через x,- его приближенное значение. Тогда разность 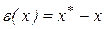 называется погрешностью приближённого числа x. При действиях с приближёнными числами обычно известно, что абсолютная величина погрешности
называется погрешностью приближённого числа x. При действиях с приближёнными числами обычно известно, что абсолютная величина погрешности 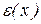 не превосходит некоторой величины
не превосходит некоторой величины 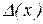 , т.е.
, т.е.
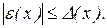
Величина 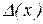 представляет собой оценку абсолютной величины погрешности и называется абсолютной погрешностью приближённого числа x. Естественно, в качестве
представляет собой оценку абсолютной величины погрешности и называется абсолютной погрешностью приближённого числа x. Естественно, в качестве 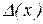 , по имеющейся информации, выбирают наименьшую величину, удовлетворяющую указанному условию. Отметим, что при наличии
, по имеющейся информации, выбирают наименьшую величину, удовлетворяющую указанному условию. Отметим, что при наличии 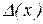 может быть установлен и диапазон расположения точного значения x. Действительно, т.к.
может быть установлен и диапазон расположения точного значения x. Действительно, т.к. 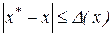 , то
, то 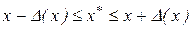 .
.
Отношение
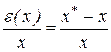
представляет собой относительную погрешность приближенного числа x. Но т.к. 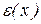 , вообще говоря, не известна, то в качестве относительной принимают верхнюю оценку
, вообще говоря, не известна, то в качестве относительной принимают верхнюю оценку 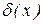 модуля этого отношения. Т.е. величина
модуля этого отношения. Т.е. величина 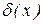 , такая, что
, такая, что
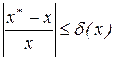
называется относительной погрешностью числа x. Очевидно, что 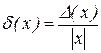 и
и 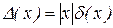 .
.
Иногда величину 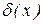 выражают и в процентах. Заметим, что при наличии
выражают и в процентах. Заметим, что при наличии 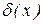 также может быть установлен диапазон расположения точного значения. Действительно, так как
также может быть установлен диапазон расположения точного значения. Действительно, так как
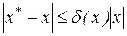 ,
,
то 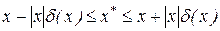 .
.
 2015-06-24
2015-06-24 688
688








