Рассмотрим разложение (6), (7). Предположим, что на отрезке 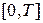 функция
функция 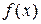 задана в m равностоящих узловых точках
задана в m равностоящих узловых точках 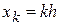 , где
, где 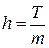 ,
, 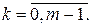
Используя для вычисления коэффициентов 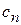 формулу левых прямоугольников из (7) имеем
формулу левых прямоугольников из (7) имеем
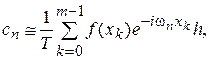
или, учитывая 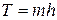 ,
,
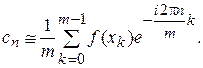 (8)
(8)
Соотношение (8) называется дискретным преобразованием Фурье.
Таким образом, учитывая 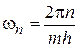 окончательно имеем
окончательно имеем
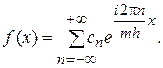
Из соотношений (8) вытекают следующие свойства.
Свойство 1. Набор коэффициентов 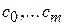 является комплексно сопряженным, т.е.
является комплексно сопряженным, т.е.
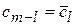 ,
, 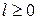 ,
,
Действительно, согласно (8), имеем
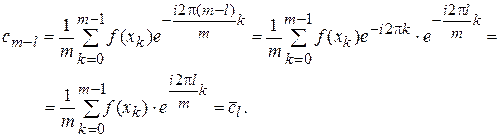
Свойство 2. Набор коэффициентов 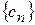 ,
, 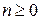 является периодическим с периодом равным m. Т.е.
является периодическим с периодом равным m. Т.е. 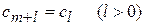 .
.
Обосновывается аналогичным образом.
Следствие. Для построения разложения (8) при численном моделировании с равноотстоящими узловыми точками достаточно вычисления 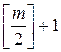 по коэффициентов
по коэффициентов 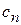 .
.
Так, при m=3, например, - коэффициентов 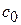 ,
, 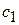 . Тогда по свойству 1,
. Тогда по свойству 1, 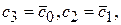 а
а 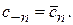 По свойству 2, -
По свойству 2, - 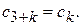 При m=4, - коэффициентов
При m=4, - коэффициентов 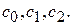 Тогда
Тогда 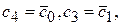
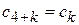 , и
, и 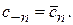
 2015-06-24
2015-06-24 345
345








