2015-06-24
241
1. Разложить указанные функции в ряд Фурье:
- в задачах 1 б), 2 б) представить разложение в стандартной форме;
- в задачах 1 а), 2 а) представить в комплексной форме.
2. Получить разложения указанных функций, используя стандартные процедуры пакета Matlab.
3. Сравнить полученные результаты для первых n гармоник.
Разложить указанные функции в ряд Фурье в указанных интервалах
Вариант 1
1. 
a) 
, 
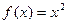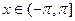б)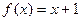 
, 
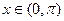по синусам,
2. а)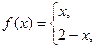 
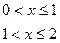б)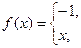 
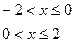по косинусам,
Вариант 2
1. a) 
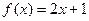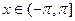, б)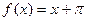 
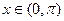, по косинусам,
2. а)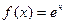 
, 
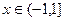б)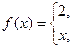 
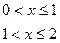по синусам.
Вариант 3
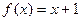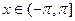1. a) , б)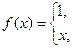 
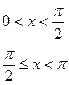, по косинусам,
2. а)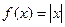 
, 
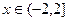б)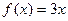 
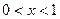по синусам.
Вариант 4
1. a) 
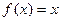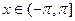, б)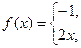 
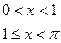, по синусам,
2. а)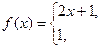 
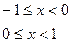, б)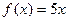 
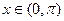, , по косинусам.
Вариант 5
1. a) 
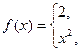
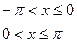, б)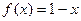 
, 
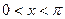по косинусам,
2. а)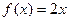 
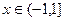, , б)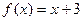 
, 
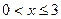, по синусам.
Вариант 6
1. a) 
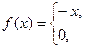
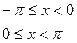, б) ,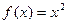 
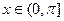по косинусам,
2. а) 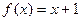, , 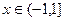б) ,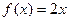 
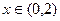по косинусам.
Вариант 7
1. a) 
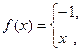
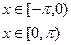, б) 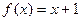, 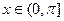по косинусам,
2. а) 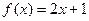, , 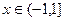б) ,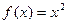 
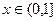по синусам.
Вариант 8
1. a) 
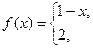
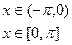, б)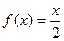 
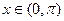, по синусам,
2. а) ,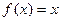 
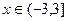, б) ,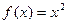 
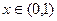по косинусам.
Вариант 9
1. a) 
, 
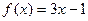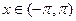, б)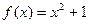 
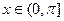, по косинусам,
2. а) ,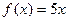 
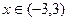, б)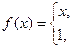 
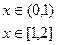по синусам.
Вариант 10
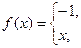
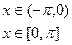1. a) , б)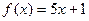 
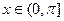, по косинусам,
2. a) 
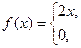
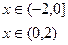, б) ,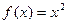 
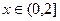по синусам.
Вариант 11
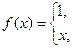
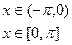1. a) , б)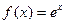 
, 
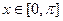по синусам,
2. a) 
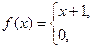
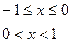, б)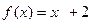 
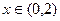, по косинусам.
Вариант 12
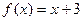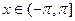1. a) , б)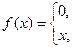 
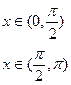по косинусам,
2. а) ,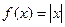 
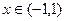б) 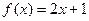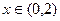по синусам.
Вариант 13
1. a) 
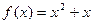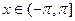, б)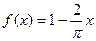 
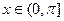, по синусам,
2. а)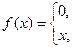 
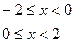б)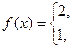 
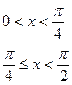по косинусам.
Вариант 14
1. a) 
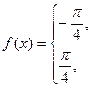
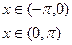, б)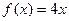 
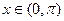, по косинусам,
2. а) 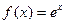, , 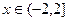б)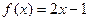 
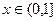, по синусам.
Вариант 15
1. a) 
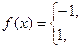
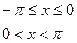, б)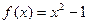 
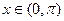, по косинусам,
2. а) 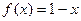, , 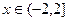б) 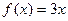, 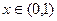по синусам.
Вариант 16
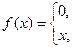
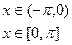1. a) , б)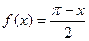 
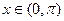, по синусам,
2. а)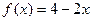 
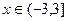, , б) 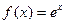, 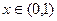по косинусам.
Вариант 17
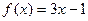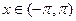1. a) , б)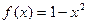 
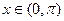по синусам,
2. а)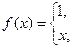 
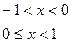, б) 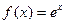, , 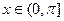по косинусам.
Вариант 18
1. a) 
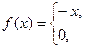
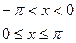, б)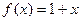 
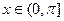, по косинусам,
2. a) 
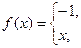
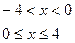, б)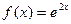 
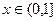, по синусам
Вариант 19
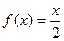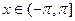1. a) , б) 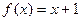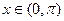, по синусам,
2. а)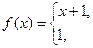 
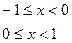, б)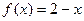 
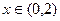, , по косинусам.
Вариант 20
1. a) 
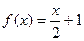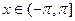, б) 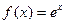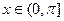по косинусам,
2. а)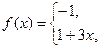 
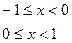, б) 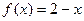, 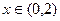по синусам.
Вариант 21
1. a) 
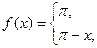
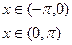, б) 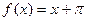, 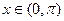по синусам,
2. а)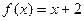 
, 
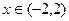, б) 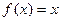, 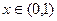по косинусам.
Вариант 22
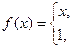
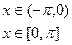1. a) , б)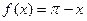 
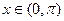, по косинусам,
2. а) ,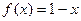 
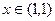, б) 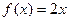, 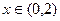по синусам.
Вариант 23
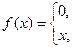
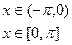1. a) , б)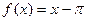 
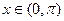, по синусам,
2. а) 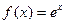, , 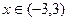б) 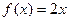, 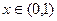по косинусам.
Вариант 24
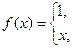
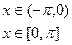1. a) , б)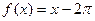 
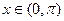, по косинусам,
2. а) 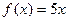, , 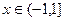б)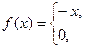 
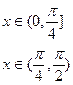по синусам.
Вариант 25
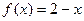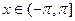1. a) , б)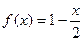 
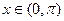, по синусам,
2. а)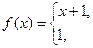 
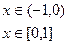, б)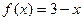 
, 
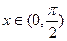, по косинусам.
Дополнительная литература
1. В.И. Крылов, В.В. Бобков, П.И. Монастырный. Вычислительные методы. В 2-х томах. – М. Наука, 1976.
2. Р.В. Хемминг. Численные методы для научных работников и инженеров. – М.: Мир, 1968.
3. Д.Н. Фаддеев, В.Н. Фаддеева. Вычислительные методы линейной алгебры. – СПб.: Издательство «Лань», 2002.
4. С.В. Поршнев. Вычислительная математика. Курс лекций. – СПб.: БХВ- Петербург, 2004.
