Решение: Покажем, что ненулевой является только цепочка 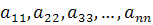 , а все остальные цепочки будут иметь множитель из тех нулей, которые расположены под диагональю.
, а все остальные цепочки будут иметь множитель из тех нулей, которые расположены под диагональю.
От противного. Пусть существует другая цепочка, не содержащая ноль. Тогда из первого столбца в этой цепочке может быть только 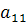 . Из второго столбца число
. Из второго столбца число 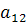 взять нельзя (так как уже взято число из первой строки), поэтому из второго столбца берется только
взять нельзя (так как уже взято число из первой строки), поэтому из второго столбца берется только 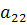 . Рассуждая аналогично, получаем цепочку
. Рассуждая аналогично, получаем цепочку 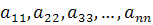 , что противоречит предложению о другой возможной цепочке.
, что противоречит предложению о другой возможной цепочке.
Ответ: 1.
Задание №2.
Решение: 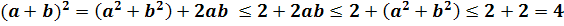 . Таким образом
. Таким образом 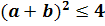 ,откуда
,откуда 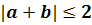 .
.
 2015-06-24
2015-06-24 209
209








