10 КЛАСС
1. ах3 + вх2 + сх = 0 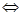 х (ах2 + вх + с) = 0
х (ах2 + вх + с) = 0 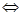
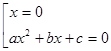 . Если а = 0, то корень второго уравнения х = -
. Если а = 0, то корень второго уравнения х = - 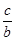 , и сумма корней исходного уравнения равна -
, и сумма корней исходного уравнения равна - 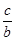 . Пусть
. Пусть
а ≠ 0 и второе уравнение совокупности имеет корни х1 и х2, причем х1 + х2 = - 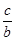 . Тогда по теореме Виета их сумма равна -
. Тогда по теореме Виета их сумма равна - 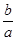 . Таким образом, -
. Таким образом, - 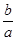 = -
= - 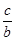
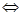
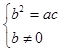 .
.
Тогда D = -3 в 2 < 0, корней нет. Противоречие.
Ответ: при а = 0, в ≠ 0 и с 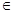 R.
R.
2. 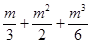 =
= 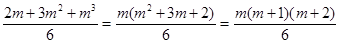 . В числителе произведение 3-х последовательных целых чисел, значит одно из них обязательно делится на 2 и одно из них делится на 3, поэтому произведение делится на 6.
. В числителе произведение 3-х последовательных целых чисел, значит одно из них обязательно делится на 2 и одно из них делится на 3, поэтому произведение делится на 6.
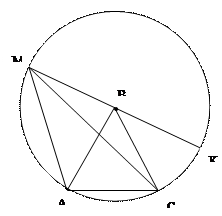 3. 1) Точка М лежит на окружности с центром в точке В и радиусом АВ (по теореме о вписанном угле).
3. 1) Точка М лежит на окружности с центром в точке В и радиусом АВ (по теореме о вписанном угле).
2) 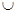 АС = 60°, так как
АС = 60°, так как 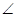 АВС = 60°.
АВС = 60°.
3) 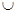 СК = 40°, так как
СК = 40°, так как 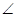 СМВ = 20°.
СМВ = 20°.
4) 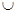 АМ =
АМ = 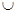 КМ -
КМ - 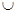 СК -
СК - 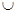 АС =
АС =
= 180°- 60° - 40° = 80°.
5) 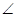 АСМ – вписанный и опирается на
АСМ – вписанный и опирается на 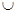 АМ
АМ 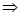
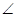 АСМ = 40°.
АСМ = 40°.
Ответ: 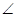 АСМ = 40°.
АСМ = 40°.
4. Предположим, что такая последовательность существует. Тогда она имеет вид:
а1; а1 + d = а1q; а1 + 2d = а1q2, где а1 ≠ 0 (что следует из определений арифметической и геометрической прогрессии).
Решим систему 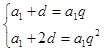
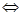
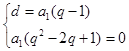 откуда q = 1, d = 0, а1
откуда q = 1, d = 0, а1 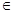 R
R 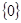 . Получаем последовательность трех одинаковых чисел, что противоречит условию.
. Получаем последовательность трех одинаковых чисел, что противоречит условию.
5. Докажем сначала, что вынув 2009 шариков, мы наверняка вытащим 670 шариков одного цвета. Пусть а – количество вынутых красных, в – зеленых, с – остальных, тогда а + в + с = 2009. Предположим от противного, что при этом нет 670 – ти шариков одного цвета, тогда а ≤ 669 и в ≤ 669, а + в + с ≤ 669 + 669 + 670 = 2008. Противоречие. Очевидно, что при меньшем количестве вынутых шариков всегда возможна ситуация, когда не будет 670-ти шариков одного цвета.
Ответ: 2009.
 2015-06-24
2015-06-24 327
327







