2015-06-24
226
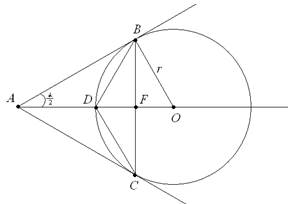
О – центр окружности радиуса r, вписанной в угол А.
F – точка пересечения отрезков DO и BC.
Известно, что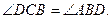 
С другой стороны, т.к. DB=DC, то 
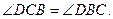Следовательно, 
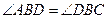, и BD – биссектриса 
Таким образом, D – центр вписанной в треугольник ABC окружности, и DF – ее радиус.
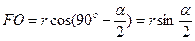
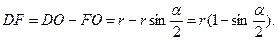
Ответ: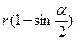 
.
Задача № 3. Будем искать искомый трехчлен в виде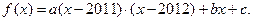 
Тогда 
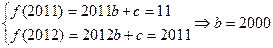и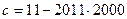 
– число нечетное. 
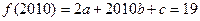, откуда 
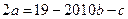– число четное. Следовательно, а – целое.
Замечания.
1) Можно показать, что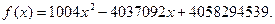 
2) Задача будет иметь положительный ответ, если задать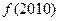 
нечетным, не меняя остальных условий.
Ответ: да.
Задача № 4. Без нарушения общности можно считать, что числа расположены по возрастанию. Тогда,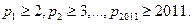 
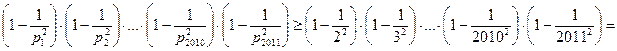
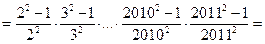
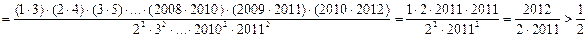
Задача № 5. Пусть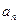 
– количество n -значных чисел, состоящих только из цифр 2 или 5, у которых две двойки не стоят рядом. Разобьем множество таких чисел на два подмножества. К первому отнесем нечетные числа (они заканчиваются на 5), ко второму – четные (они заканчиваются на 52). Считаем, что n ≥3. В первом подмножестве уберем последнюю цифру 5. Получим все возможные (n- 1)-значные числа, удовлетворяющие условию. Их количество – 
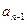. Во втором подмножестве уберем последние две цифры 52. Получим все возможные (n-2)-значные числа, удовлетворяющие условию. Их количество – 
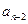. Таким образом, 
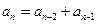. Очевидно, 
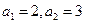. Тогда 
.
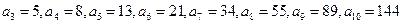Ответ: 144.
