1.1. Определить размерность следующих матриц:
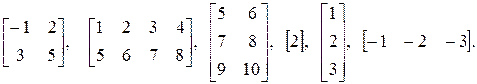
1.2. Какие из следующих матриц являются диагональными, верхними треугольными, нижними треугольными:
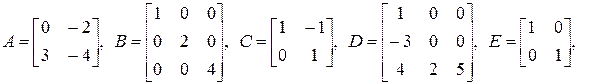
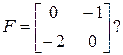
1.3. Дана матрица 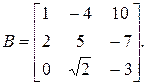 Чему равны элементы
Чему равны элементы 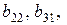
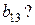 Какие элементы образуют главную диагональ, какие – побочную?
Какие элементы образуют главную диагональ, какие – побочную?
1.4. Найти 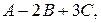 если:
если:
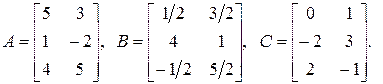
1.5. Найти матрицу Х из уравнения:
а) 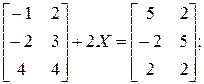 б)
б) 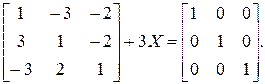
1.6. Найти АВ и установить, существует ли ВА, если
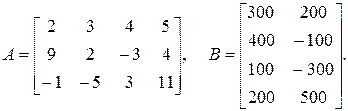
1.7. Найти АВ и ВА, если:
а) 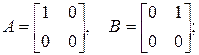 б)
б) 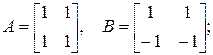
в) 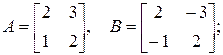 г)
г) 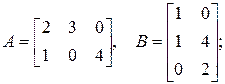
д) 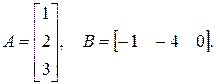
Сделать вывод о выполнении равенства АВ = ВА.
1.8. Даны матрицы 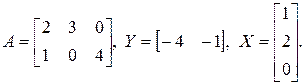 Найти те попарные произведения данных матриц, которые существуют.
Найти те попарные произведения данных матриц, которые существуют.
1.9. На примере матриц А и В убедиться, что 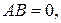 хотя
хотя 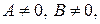 если:
если:
а) 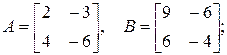
б) 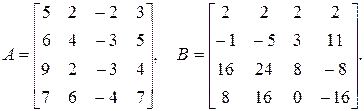
1.10. Дано:
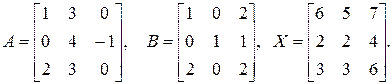
Показать, что АХ = ВХ, хотя 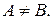
1.11. Найти 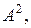 если
если 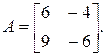
1.12. Показать, что операция транспонирования матрицы обладает свойствами:
а) 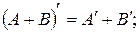 б)
б) 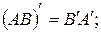 с)
с) 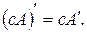
1.13. Найти 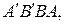 если:
если:
а) 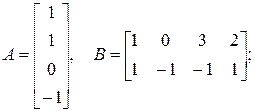 б)
б) 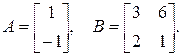
1.14. Дано:
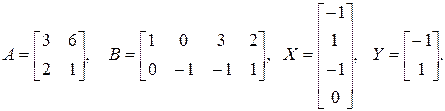
Найти 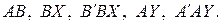
1.15. Даны матрицы:
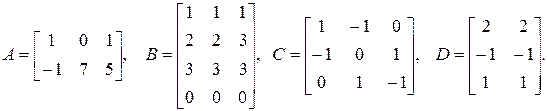
Определить размерность следующих матриц: AC, AD, DA, BC, CB, DAC, BCDA. Найти:
1) элемент, стоящий во второй строке и втором столбце матрицы АС;
2) элемент, стоящий в четвертой строке и первом столбце матрицы ВС;
3) элемент, стоящий в последней строке и последнем столбце матрицы DA;
4) элемент, стоящий в первой строке и первом столбце матрицы ВС.
1.16. Пользуясь свойствами умножения матриц, вычислить наиболее рационально АВ, если 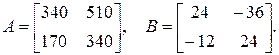
1.17. Даны матрицы 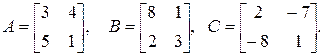 Найти матрицу
Найти матрицу 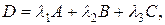 если
если 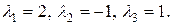
1.18. Найти 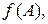 если:
если:
а) 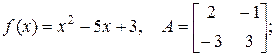
б) 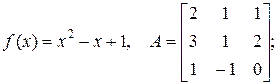
в) 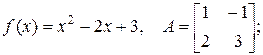
г) 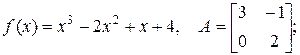
д) 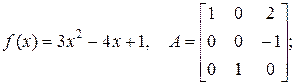
е) 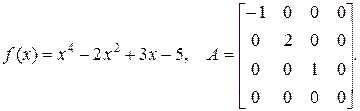
1.19. Найти 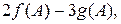 если
если 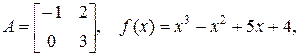
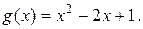
1.20. Найти 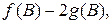 если
если 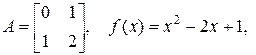
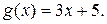
1.21. Найти 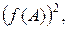 если
если 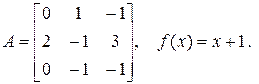
1.22. Найти 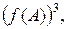 если
если 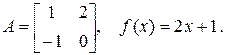
1.23. Выполнить указанные действия:
а) 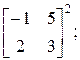 б)
б) 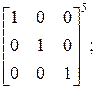 в)
в) 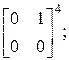 г)
г) 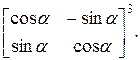
1.24. Вычислить выражения при 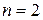 и
и 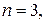 обнаружить закономерность и с помощью метода математической индукции обосновать ответ:
обнаружить закономерность и с помощью метода математической индукции обосновать ответ:
а) 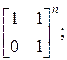 б)
б) 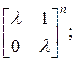 в)
в) 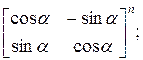 г)
г) 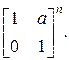
ОТВЕТЫ
 2015-06-24
2015-06-24 2057
2057