Решение некоторых задач алгебры матриц

Напомним основные определения алгебры матриц. Если т*п выражений расставлены в прямоугольной таблице из т строк и п столбцов, то говорят о матрице размера т * п. Выражения а_ij, называют элементами матрицы. Элементы а_ij (i=1,…n), стоящие в таблице на линии, проходящей из левого верхнего в правый нижний угол квадрата п* п, образуют главную диагональ матрицы. Матрица размером т*п(т≠ п) называется прямоугольной. Если т=п, то матрицу называет квадратной порядка п. В частности, матрица типа 1 * п - это вектор-строка, а матрица размером т* 1 является вектором-столбцом. Число (скаляр) можно рассматривать как матрицу типа 1*1.

Квадратная матрица А = { a_ij } размером п * п называется:

■ нулевой, если все ее элементы равны нулю А = { а_ij = 0 };

■ верхней треугольной, если все элементы, расположенные ниже главной диагонали, равны нулю А = { а_ij = 0, для всех i>j };

■ нижней треугольной, если все элементы, расположенные выше главной диагонали, равны нулю А = {а_ij = 0, для всех i >j);

■ диагональной, если все элементы, кроме элементов главной диагонали, равны нулю А = {а_ij =0, для всех i≠j};

■ единичной, если элементы главной диагонали равны единице, а все остальные - нулю А = { a_ij = 0, для всех i≠j и a_ij= 1 для всех i=j,

■ cквадратной матрицей связано понятие определителя, или детерминанта. Определителем матрицы А является число det A или D, вычисляемое по правилу:

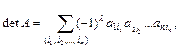
где сумма распределена на всевозможные перестановки (i₁, i₂,… i_n)элементов 1, 2,... п и, следовательно, содержит п слагаемых, причем 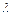= 0, если перестановка четная, и 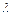= 1, если она нечетная. Квадратная матрица называется невырожденной, если ее определитель отличен от нуля. В противном случае она называется вырожденной, или сингулярной.

С матрицами можно проводить операции сравнения, сложения и умножения. Две матрицы А = {а_ij} и В = {b_ij.) считаются равными, если они одного типа, то есть имеют одинаковое число строк и столбцов и соответствующие элементы их равны { а_ij } = { b_ij }. Суммой двух матриц А = {а_ij} и В = {b_ij} одинакового типа является матрица С= {с_ij} того же типа, элементы которой равны сумме соответствующих элементов матриц А = {а_ij} и B = {b_ij}, то есть { с_ij} = {а_ij+b_ij}. Разность матриц определяется аналогично. Произведением числа 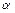на матрицу А = {а_ij} (или произведением матрицы на число) называется матрица, элементы которой получены умножением всех элементов матрицы А на число 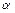, то есть А = A 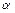= А{ 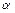* а_ij}. Произведением матриц А = {а_ij) размерностью m*n и B= {b_ij} размерностью р*s является матрица С размерностью т х s, каждый элемент которой можно представить формулой { с_ij }= {a_i₁b₁_j+ a_i₂b₂_j+... + a_inb_in, i= 1, ...m, j=1,..,s}. Таким образом, произведение матриц АВ имеет смысл только тогда, когда количество строк матрицы А совпадает с количеством столбцов В. Кроме того, произведение двух матриц не подчиняется переместительному закону, то есть АВ≠ ВА. В тех случаях, когда АВ = ВА, матрицы А и В называются перестановочными.

Если в матрице А = {а_ij} размерностью т*n «заменить строки соответствующими столбцами, то получится транспонированная матрица А^T = [а_ij]. В частности, для вектора-строки транспонированной матрицей является вектор-столбец.

Обратной матрицей по отношению к данной А = {а_ij) размерностью n*n, называется матрица А^-1 = { А_ij } того же типа, которая, будучи умноженной как справа, так и слева на данную, в результате дает единичную матрицу Е = {d_ij}:A*A^-1= А^-1*А= Е. Нахождение обратной матрицы для данной называется обращением данной матрицы. Всякая неособенная матрица имеет обратную.