Здесь должны быть рисунки – иллюстрации к определениям

Эквивалентности, записанные в правых частях, следует рассматривать как следствия определений. Доказательства требуют только условия симметричности и транзитивности. Рассмотрим цепочку определений:

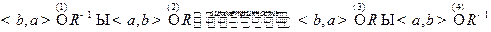
Из (2,3,4) следует RÍR^-1, а из (1,2,3) – обратное включение R^-1ÍR.

NB. Определение антисимметричных отношений допускает равенство R^-1∩R= Ø.

Докажем включение R²ÍR для транзитивных отношений. Пусть aR²b, т.е. существует элемент с такой, что aRc & cRb – по определению композиции. Но, по определению транзитивности, получаем следствие: aRb.

• Бинарные отношения равенства и конгруэнтности (подобия) на множестве геометрических фигур рефлексивны: каждый треугольник или квадрат равен или подобен самому себе.
• Отношение равенства на любых множествах рефлексивно: а = а.
• Также рефлексивны отношения нестрогого неравенства ≤, ≥ на множестве действительных чисел. Вообще, любое отношение, включающее равенство – рефлексивно. Пример – похожесть людей.
• Напротив, строгие неравенства <, > и включения множеств – иррефлексивны.
• Особо отметим отношение Í, Ì включения множеств – одно рефлексивно, другое нет. Эти отношения естественным образом определены на множестве всех подмножеств данного множества – или универсума (на соответствующем булеане). Таким образом, одно из начальных понятий теории множеств приводит к появлению некоторой структуры, или иерархии, или порядка на множествах.
• Не следует смешивать иррефлексивные и нерефлексивные отношения: иррефлексивные всегда и нерефлексивные, но не наоборот – нерефлексивное отношение может включать часть диагонали.
• Все отношения равенства и подобия симметричны: если один треугольник подобен второму, то и второй подобен первому.
• Бинарные отношения равенства и включения, как строгие, так и нестрогие – антисимметричны.

• Пусть М – множество населённых пунктов. Зададим на нём бинарное отношение достижимости →: из пункта А достижим пункт Б, если их связывает (железная) дорога. Очевидно, если А→Б и Б→С, то и А→С. Отметим, что транзитивность сохраняется даже если дорога односторонняя, т.е. при несимметричном →.
• Равенство и подобие в геометрии транзитивны.
• Бинарные отношения перпендикулярности прямых и не равенства чисел нетранзитивны.
• Похожесть людей, отношение дружбы, дипломатические отношения – нетранзитивны.

Бинарное отношение R на множестве А называется плотным, если

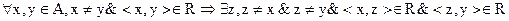
Попросту говоря, для любой пары элементов, связанных отношением, найдётся хотя бы один (и, следовательно, бесконечно много) элемент «между» ними. Пример – отношение неравенства на действительных числах, но не на целых. Для плотных отношений справедливо включение

RÍ R².

Следствие: транзитивное плотное отношение удовлетворяет равенству: R²= R.

Среди всех бинарных отношений на произвольном множестве специально выделяют отношения, обладающие совокупностью вышеперечисленных свойств. Таковыми являются:

Отношение эквивалентности: