Функциональная полнота

Класс функций F называется полным в Р (пространстве булевых функций, например), если замыкание [F] совпадает в с Р. По-другому: Любая булева функция может быть реализована в виде формулы над F.

Следствием теорем о совершенных формах является важнейшее свойство булевых функций, которое мы сформулируем в виде отдельной теоремы.

Теорема.

Любая булева функция может быть реализована в виде формулы над базисом {,Ú, Ù}.

►Утверждение доказано для всех функций, кроме 0. Нуль представим в виде: xÙx=0. ◄

– Эта теорема решает проблему полноты как в общем смысле, так и для частного выбора функций – стандартного базиса.

Для практических нужд необходимо найти как можно больше полных систем функций. Возможно полное решение такой задачи: дана система функций. Требуется определить, полна ли система и если да, то возможно ли уменьшить ее, оставляя полной. Частным решением этого вопроса служит

Теорема: Пусть даны две системы функций: F и G. Тогда, если система F полна и все функции из F реализуются формулами над G, то система G также полна.

Теорема доказывается простой подстановкой (суперпозицией) формул.

Перечислим полные системы элементарных функций.

Теорема: Следующие системы функций полны:

1. {,Ù,Ú} – стандартный базис.

2. {,Ú}

3. {,Ù}

4. {|}

5. {↓}

6. {0,1, Ù, Å}

► 2), 3): xÙy ≡ (xÙy) и наоборот;

4) x ≡ (x|x), xÙy ≡ (x|y) ≡ (x|y)|(x|y):

5) x ≡ (x↓x), xÚy ≡ (x↓y) ≡ (x↓y) ↓ (x↓y)

6) x ≡ xÅ1, xÚy ≡ xÙyÅxÅy. ◄

Теорема. СДНФ, СКНФ и полином Жегалкина для любой булевой функции определены однозначно.

► Рассмотрим уравнение 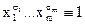. Из определения следует, что данное уравнение имеет единственное решение x_i = σ_i, i = 1,…,n. Поэтому и уравнение f(x₁,…,x_n) ≡ 1 имеет единственное решение (с точностью до перестановки слагаемых), равное дизъюнкции конституент носителя:

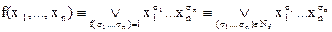. (Это использование взаимной однозначности соответствия f↔N_f.)

· Единственность СКНФ следует по теореме двойственности из единственности СДНФ.

· Единственность полиномов следует из того, что алгебра Жегалкина изоморфна полю вычетов по модулю 2 (или, эквивалентно, разложение 0 имеет все нулевые коэффициенты).

Разложение булевых функций над базисом Жегалкина по этой причине называют СПНФ.

Таким образом, к совершенным формам СДНФ и СКНФ добавилась еще одна система – полиномов Жегалкина (СПНФ). Общий вид полинома Жегалкина следующий:

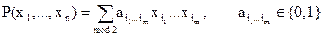
Например, при n=3 будем иметь выражение:

a₁₂₃x₁x₂x₃ Å a₁₂x₁x₂Å a₁₃x₁x₃ Å a₂₃x₂x₃ Å a₁x₁Å a₂x₂ Å a₃x₃ Å a₀.

· Общее число полиномов Жегалкина – 2 в степени 2ⁿ – совпадает с числом булевых функций и складывается из 2ⁿ – общего числа коэффициентов и 2-х возможных значений каждого коэффициента.

· Для вычисления коэффициентов полинома необходимо решать системы линейных уравнений над полем вычетом по модулю 2. Называется это методом неопределенных коэффициентов.

Пример. Пусть вектор значений булевой функции f равен 11001011. Найдем полином Жегалкина, представляющий f. Поскольку размерность вектора значений равна 8, то f задана как функция от 3-х переменных. Тогда она представлена полиномом Жегалкина 3-й степени, общий вид которых дает предыдущая формула. Составим систему уравнений в поле Z₂:

0) f(000) = 1 → a₀ =1;

1) f(001) =1, f(010) = 0, f(100) = 1→ a₃Åa₀=a₁Åa₀ = 1, a₂ Åa₀=0;

2) f(110) =1, f(101) = f(011) = 0 → a₁₂Åa₁Åa₂Åa₀=1, a₂₃Åa₂Åa₃Åa₀=0, a₁₃Åa₁Åa₃Åa₀=0;

3) f(111) =1 → a₁₂₃Åa₁₂Åa₁₃Åa₂₃Åa₂Åa₀ =1;

Итак, f = x₁x₂x₃Åx₁x₂Åx₁x₃Åx₂Å1.

Рассмотренные теоремы позволили построить алгоритм, разрешающий формулу алгебры логики. Алгоритм фактически основан на свойстве полноты 3-х основных операций булевой алгебры. — Любая булева функция может быть представлена в виде формулы над функциями {, &, Ú}.

Проблема полноты может быть поставлена в более общем виде.

Определение. Класс (множество) булевых функций F = {f₁, f₂, …,f_n,…} называется функционально полным, если любая булева функция может быть представлена в виде формулы над F.

Теорема. Пусть даны две системы функций: F = {f₁, f₂, …,f_n,…} и G = {g₁, g ₂, …, g _n,…}, относительно которых известно, что а) система F полна; б) каждая функция системы F выражается в виде формулы над G. Тогда система G полна.

Следствие: системы {, &,.}, {, &}.{,.}, {→, 0}, {Å, &, 0, 1}, {|},{↓} полны.

Пример показывает, что существует много полных классов функций, каждый из которых можно принять за множество элементарных функций и на нём строить язык логики высказываний. Какой именно из языков использовать – зависит от характера задачи и пристрастий исследователя. — Алгеброй Буля можно называть и {|}! Так, относящийся к логике вопрос синтеза СФЭ приводит к сложным задачам, если на число элементарных функций в наборе накладываются ограничения.

Последующее изложение представляет результаты Поста.

Наша цель – найти критерий полноты произвольной системы функций или, по-другому, решить задачу: дан произвольный набор функций F={f₁, …,f_s,…}. Верно ли, что [F]=P₂? Для того, чтобы решить эту задачу, оказалось удобным сначала решить противоположную задачу: найти все наборы функций такие, что [F]¹P₂. Другими словами, следует найти сначала все неполные замкнутые классы функций. Пост выяснил, что все неполные замкнутые классы «группируются» в пять основных классов, называемых классами Поста. Эти классы обладают следующими свойствами.

Определение. Класс R называется предполным, или максимальным, если R неполон, а для "fÏR класс RÇ{f} полон.

Следовательно, любой неполный замкнутый класс должен содержаться целиком хотя бы в одном из классов Поста.

Следовательно, любой полный класс не должен содержаться целиком в каждом классе Поста: "i FÚR_i. Это и есть решение задачи: берём произвольный класс F и ищем в нём функции, не принадлежащие классам Поста. Если таковые находятся – класс полон.

Предполными классами являются следующие классы Поста и только они:

1. T₀ = {f | f(0,0,…,0) = 0} – класс функций, сохраняющих константу 0.

2. T₁ = {f | f(1,1,…,1} = 1} – класс функций, сохраняющих константу 1.

3. S = {f| f = f*} – класс самодвойственных функций.

4. M = 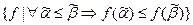– класс монотонных функций.

5. L – класс линейных функций.

Примеры функций из каждого класса:

	T0	T1	S	M	L
	+	–	–	+	+
	–	+	–	+	+
x	+	+	+	+	+
x	–	–	+	–	+

Отметим, что все классы попарно различны, а конъюнкция и дизъюнкция – не линейные функции.

Лемма 1.

Если булева функция 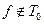, то из неё можно получить: либо а) константу 1, либо б) отрицание x.

Пусть 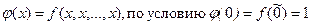. Сравним со значением функции в 1:

.

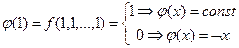Лемма 2.

Если булева функция 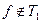, то из неё можно получить: либо а) константу 0, либо б) функцию отрицания. — Проще всего для доказательства леммы воспользоваться двойственностью.

Лемма 3.

Если булева функция 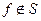, то из неё подстановкой х и x можно получить константы 0 и 1.

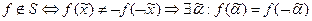. Пусть 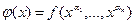. Тогда получаем:

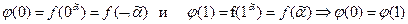. Вторая константа получается из данной операцией отрицания.

Лемма 4.

Если 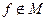, то из неё подстановкой констант 0,1 и тождественной функции х можно получить отрицание x.

Лемма 5.

Если 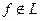, то из неё путём подстановки констант 0, 1 и функций вида х, x и, быть может, навешиванием отрицания, можно получить функцию x₁&x₂.

Идея доказательства: в нелинейной функции есть члены квадратичные (то, что надо), или высших степеней. Из членов высших степеней можно подстановкой констант спуститься до квадратичных членов – а затем выделить конъюнкцию.

Теорема о функциональной полноте.

Для того чтобы система F была полной, необходимо и достаточно, чтобы она целиком не содержалась ни в одном из пяти замкнутых классов.

2-я формулировка: для полноты системы необходимо и достаточно, чтобы для каждого класса Поста Т₀, Т₁, S, M, L среди функций системы нашлась функция, не принадлежащая данному классу.

3-я формулировка: в критериальной таблице в каждом столбце должен найтись «–».

Пример:

	T0	T1	S	M	L
	+	–	–	+	+
→	–	+	–	–	–
~	–	+	–	–	+
Ú	+	+	–	+	–
Ù	+	+	–	+	–
Å	+	–	–	–	+

{0,→} - система полна. Система {0,., ~} – также полна; это система, двойственная к {1, Ù,Å} – базису Жегалкина.

Необходимость следует из неполноты каждого класса.

Достаточность (идея доказательства): выберем из класса 5 функций, каждая из которых не принадлежит некоторому классу (попарно различному).

I. По лемме 1 из 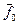можно получить либо 1, либо x, по лемме 2 из 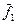– либо 0, либо x. Всего получается 4 варианта:{0, 1}, {0, x}, {1, x}, {x}

II. Варианты 2-й и 3-й (0 =1, 1 = 0) приводят к набору функций {0, 1, x}.

III. Применение леммы 4 к 1-му варианту с использованием 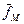приводит к тому же набору.

Применение леммы 3 к 4-му варианту с использованием 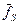приводит к тому же набору.

IV. Из набора {0, 1, x} и функции 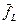по лемме 5 получается конъюнкция.

Таким образом, при помощи функций из классов Поста реализованы функции x и x&y – следовательно, набор из 5-ти функций, не водящих в классы Поста, полон.

Из доказательства теоремы непосредственно вытекает следующая теорема.

Теорема. Из всякой полной системы функций можно выделить полную подсистему, содержащую не более 4-х функций.

Функция 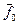дополнительно обладает свойством: она либо несамодвойственна, либо не сохраняет 1 и немонотонна. Поэтому полной будет либо система { 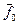, , 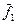, 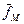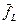}, либо { , , }.

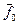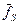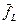Пример показывает, что константа 4 не может быть понижена.

Теорема о функциональной полноте на самом деле даёт не только критерий полноты. Она позволяет найти для произвольной булевой функции f формулу через функции полной системы.

Ещё некоторые следствия доказанных теорем.

Определение. Система функций {f₁, f₂,…,f_s,…} из замкнутого класса R называется его базисом, если она полна в R, но всякая её подсистема не является полной в R.

Так, система

f₁ = x₁x₂, f₂ = 0, f₃ = 1, f₄ = x₁Åx₂Åx₃

является базисом в Р₂. Можно показать, что система {0, 1, x₁Ùx₂, x₁Úx₂} является базисом для М.

Теорема. Каждый замкнутый класс из Р₂ имеет конечный базис.

Теорема. Мощность множества замкнутых классов в Р₂ – счётная.