Общие сведения. Графы – классический объект дискретной математики, введённый в науку ещё Эйлером

Графы – классический объект дискретной математики, введённый в науку ещё Эйлером. Понятия и результаты теории графов широко и часто используются в конкретных дисциплинах, в том числе и нематематических. Поэтому многие свойства графов получены не в работах чистых математиков, а в конкретных приложениях, зачастую by product. В результате теория графов представляет собой довольно большой конгломерат отдельных результатов, а не стройную теорию. Осложняется изучение графов ещё тем, что разные авторы используют разную терминологию по отношению к одним и тем же объектам, и даже один и тот же автор может использовать совершенно разную терминологию для минимально различающихся объектов – например, по отношению к графам и орграфам. Суть же, если она есть, совсем не в том, как мы будем называть линию, соединяющую вершины – ребром, дугой или ещё как.

Всем известны объекты, которые в математике считаются графами. Это:

а) схема метрополитена;

б) карта железных и/или автодорог;

в) радио/электронные схемы;

г) блок-схемы устройств, программ;

д) изображение процессов в физике;

е) структурные формулы в химии, например: Н — О — Н;

ж) взаимное влияние кроликов и лис;

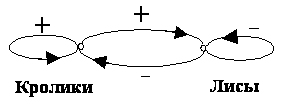
з) сетевые графики работ;

и) задача: разрезаем лист бумаги на несколько частей, затем некоторые из обрезков ещё, потом ещё несколько раз. Сколько всего получится обрезков? — Решается построением графа.

Эти примеры демонстрируют основное свойство графов – наглядность изображения устройства, процесса и т.п. Но в то же время графы являются не только иллюстрацией чего-либо, но и зачастую являются объектом, без которого нельзя обойтись. Примеры – электронные схемы, диаграммы Фейнмана … и многое другое…

В предъявленных примерах графов можно усмотреть некоторые общие черты. Отметим следующие свойства графов:

· несущественны длина и взаимное расположение линий – важно лишь, есть линия или нет;

· существенно количество линий, выходящих из вершины;

· в графах могут присутствовать вершин и линии разного типа, в т.ч. им может быть приписаны числа, знаки, цвета, типы и т.д. – это могут быть км, рубли, тыс. чел., …

Эти свойства показывают, что граф есть объект, составленный из двух объектов: множества вершин и совокупности соединяющих их рёбе р. Почему совокупности? Потому что:

· может быть несколько ребер, соединяющих две вершины – тогда Е должно считаться не множеством, а мультимножеством; граф в этом случае также называют мультиграфом;

· рёбра могут быть разными: окрашенными, со стрелками, знаками, нагружены и т.д.;

· граф может быть с петлями (псевдограф);

· вершины сами могут быть множествами и графами и т.д.

Определение. Графом называется алгебраическая система G = <V, E >, где V – множество вершин, а E – мультимножество ребер.

NB. Системой граф назван потому, что каждое ребро (как ориентированное, так и неориентированное) является отношением на множестве вершин ((v,u) или {v,u} соответственно).

Заметим, что иногда отождествляют неупорядоченную пару вершин {v,u} с двумя упорядоченными (v,u)Ç(u, v) – это, как правило, не соответствует задаче.

Изображение графа иногда называют диаграммой.

Изоморфизм графов – отношение эквивалентности, задаваемое биекцией h: V₁aV₂:

e₁=(u, v)Î E₁ ® e₂ = (h(u), h(v))Î E₂ & e₂=(u, v)Î E₂ ® e₁ = (h^–1(u), h^–1(v))Î E₁.

Примеры изоморфных и неизоморфных графов:

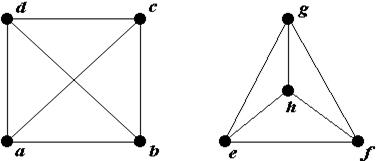
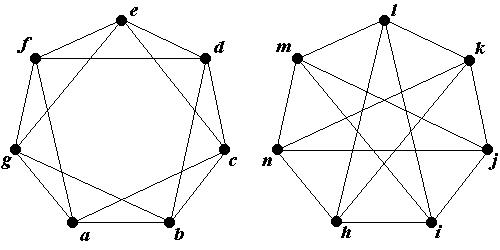
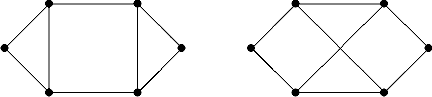
По характеристикам графа, таким как число ребер и вершин, ничего нельзя сказать об изоморфизме. Для неизоморфных графов эти числа совпадают.