Принципы построения численных методов поиска условного экстремума

Рассмотрим общую постановку задачи поиска условного экстремума со смешанными ограничениями.

Даны дважды непрерывно дифференцируемые целевая функция f (х) = (x 1, …, xn) и функции ограничений gj (x) = 0, j = 1,..., m; gj (x) ≤ 0, j = m + 1,..., p, определяющие множество допустимых решений X.

Требуется найти локальный минимум целевой функции на множестве X, т. е. такую точку х *∈ Х, что

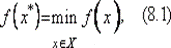
где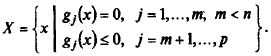

Для решения большинства практических задач используются численные методы, которые делятся на две группы.

1. Методы, использующие преобразование задачи условной оптимизации в последовательность задач безусловной оптимизации путем введения в рассмотрение вспомогательных функций: методы последовательной безусловной минимизации.

2. Методы непосредственного решения задачи условной оптимизации, основанные на движении из одной допустимой точки, где выполнены все ограничения, к другой допустимой точке с лучшим значением целевой функции. Эти методы часто называются методами возможных направлений.

Основная идея методов первой группы состоит в том, чтобы аппроксимировать исходную задачу условной оптимизации некоторой вспомогательной задачей, решение которой менее сложно, чем решение исходной. Естественно, что ограничившись одной вспомогательной задачей, можно получить, вообще говоря, лишь приближенное решение. Если же использовать последовательность задач, в определенном смысле «сходящихся» к исходной, то искомое точное решение в большинстве случаев окажется пределом соответствующей последовательности приближенных решений.

На первый взгляд кажется странным, что предлагается решать бесконечную последовательность задач оптимизаций, а не всего одну задачу. Дело в том, что на практике для получения решения исходной задачи с требуемой точностью достаточно бывает решить конечное (относительно небольшое) число вспомогательных задач. При этом нет необходимости решать их точно, а информацию, полученную в результате решения очередной вспомогательной задачи, обычно удается эффективно использовать для решения следующей;

В рамках единой методологии можно выделить несколько подходов к решению задачи.

Первый называется методом штрафов (внешних штрафов). В этом методе к целевой функции добавляется функция, интерпретируемая как штраф за нарушение каждого из ограничений. Метод генерирует последовательность точек, которая сходится к решению исходной задачи.

Второй подход называется методом барьеров (внутренних штрафов). Здесь к целевой функции исходной задачи добавляется слагаемое, которое не позволяет генерируемым точкам выходить за пределы допустимой области.

Третий подход связан с добавлением штрафной функции не к целевой функции, а к ее функции Лагранжа. В результате возникает модифицированная функция Лагранжа, а методы, использующие эту функцию, называются методами множителей.

Четвертый подход базируется на введении так называемых точных штрафных функций, позволяющих ограничиться решением лишь одной задачи безусловной минимизации.

Методы непосредственного решения задачи условной оптимизации, образующие вторую группу, связаны с нахождением предела х *последовательности { х k } допустимых точек при k → ∞, таких, что f (х k +1) < f (х k), k = 0, 1, …

Последовательность { х k } строится по правилу

х k +1= х k + δ х k, k = 0, 1, …,

где вектор δ х k определяется в зависимости от применяемого метода.

Частным случаем задачи поиска условного экстремума является задача линейного программирования, в которой целевая функция и ограничения линейны по х. Область допустимых решений представляет собой выпуклый многогранник, имеющий конечное число вершин. Процедура поиска решения заключается в переходе от одной вершины к другой, так чтобы значение функции улучшалось. Процедура поиска завершается в случае, когда из текущей вершины будет невозможен переход, связанный с улучшением функции.

Во многих практических задачах линейного программирования требуется, чтобы используемые в них переменные были целыми. Такие задачи называются задачами целочисленного линейного программирования.

2. Если текущая точка близка к границе, определяемой одним из ограничений, и если это ограничение не используется в процессе нахождения направления поиска, то может случиться так, что удастся сделать только маленький шаг и точка окажется на границе, определяемой этим ограничением. Поэтому в качестве множества Ja активных ограничений следует брать совокупность индексов почти активных ограничений: Ja = { j | – ε < gj (x) ≤ 0 }, где ε > 0 — достаточно малое число. При этом решение задачи поиска возможного направления спуска даст вектор, который обеспечивает сравнительно большие возможности для движения в рамках допустимой области.