Периодическое открытие новых автобусных маршрутов, связанное с формированием пассажиропотоков в новых жилых и промышленных районах, оказывает существенное влияние на функционирование действующей маршрутной системы автобусного транспорта города. В связи с этим возникает периодическая необходимость уточнения, совершенствования и оптимизации всей маршрутной системы города в целом. Оптимизация маршрутной системы осуществляется с помощью экономико-математических методов планирования, при этом используются два основных методических подхода.
В одном из них рассматривают маршрутную систему в совокупности с наличным парком автобусов и установленными нормативами скорости движения по участкам маршрута. В результате выявляются общие затраты времени пассажиров на поездки и их систематическое сокращение принимается в качестве основного критерия.
При втором подходе маршрутную систему автобусного транспорта города рассматривают как взаимоувязанную конфигурацию прямых транспортных связей между взаимодействующими (тяготеющими) конечными и основными промежуточными пунктами массового передвижения пассажиров на всей территории города. При этом основным критерием является минимум пересадочности. Поскольку маршрутная система базируется на транспортной сети, ее совершенствуют путем выбора лучшего варианта при равных условиях обеспеченности подвижным составом. Таким образом, второй методический подход является более рациональным, отвечающим цели и постановке задачи.
Рассмотрим алгоритм (последовательность действий) ее решения:
− на плане города с границами районов отмечают важнейшие узлы (площади) массового формирования пассажиропотоков; осуществляют ранжирование пассажирообразующих узлов (пунктов) по ожидаемым трудовым и культурно-бытовым поездкам и выявляется их примерный объем (спрос на перевозки);
− определяют первоочередные кратчайшие транспортные связи (маршруты) по перевозке пассажиров в часы пик (к местам приложения труда), а также связи районов с железнодорожными (речным, морским, автомобильным) вокзалами, рынками, станциями метрополитена и др.;
− территорию городских районов разбивают на микрорайоны и устанавливают первоочередные конечные пункты автобусных маршрутов. Выявляют первоочередность прямых транспортных связей между отдельными конечными пунктами, как для трудовых, так и культурно-бытовых поездок;
− устанавливают наиболее важные промежуточные узлы большой сменяемости пассажиров между конечными пунктами основных автобусных маршрутов, производят выбор и обоснование наиболее рациональных вариантов ожидаемой трассы маршрута;
− определяют примерное ожидаемое распределение пассажиропотока по промежуточным узловым пунктам автобусных маршрутов. Составляют примерную матрицу ожидаемых корреспонденций пассажиров между конечными и промежуточными пунктами автобусных маршрутов во времени суток. Выявляют наиболее рациональную маршрутную систему автобусного транспорта города, имеющую наибольшую прямолинейность маршрутов и минимальный коэффициент пересадочности.
Конфигурация автобусных линий на плане города образует автобусную транспортную сеть города. Автобусная транспортная сеть со всеми пролегающими по ней городскими автобусными маршрутами представляет собой маршрутную систему.
Оптимальная, с точки зрения затрат времени пассажиров на передвижение, маршрутная система должна быть проложена по кратчайшей транспортной сети. Задача нахождения кратчайшей транспортной сети сводится к задаче о минимальном покрывающем дереве в графе.
Содержательная постановка задачи заключается в следующем. Необходимо разработать проект транспортной сети, которая должна соединить конечное число микрорайонов в некотором городе. Из экономических соображений требуется, чтобы общая стоимость реализации проекта (общая протяженность сети) была минимальной, при этом должно быть выполнено обязательное условие – из любого микрорайона по данной транспортной сети можно было бы попасть в любой другой микрорайон города.
Дадим математическую постановку задачи о минимальном покрывающем дереве в графе.
Рассмотрим неориентированный связный граф: 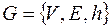 , в котором
, в котором 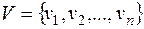 – конечное множество вершин,
– конечное множество вершин, 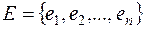 – конечное множество ребер,
– конечное множество ребер, 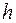 – весовая функция ребер. Для математической постановки задачи удобно обозначить отдельные значения весовой функции ребер через:
– весовая функция ребер. Для математической постановки задачи удобно обозначить отдельные значения весовой функции ребер через: 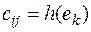 , где ребро
, где ребро 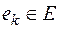 соответствует паре вершин
соответствует паре вершин 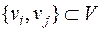 . Согласно содержательной постановке рассматриваемой задачи отдельные значения:
. Согласно содержательной постановке рассматриваемой задачи отдельные значения: 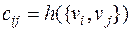 могут интерпретироваться как затраты времени пассажиров на передвижение по участку
могут интерпретироваться как затраты времени пассажиров на передвижение по участку 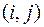 исходного графа.
исходного графа.
Стоимость любого подмножества ребер 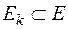 в графе
в графе 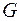 равна сумме весов ребер, входящих в это подмножество. Требуется определить такое подмножество ребер, которое образует покрывающее или остовное дерево в графе
равна сумме весов ребер, входящих в это подмножество. Требуется определить такое подмножество ребер, которое образует покрывающее или остовное дерево в графе 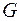 и обладает минимальной стоимостью.
и обладает минимальной стоимостью.
Для формальной записи условий задачи о минимальном покрывающем дереве в графе в виде модели булева программирования следует воспользоваться двумя условиями покрывающего дерева в графе:
1. Каждая из вершин исходного графа должна иметь хотя бы одно инцидентное ей ребро, входящее в минимальное покрывающее дерево. В противном случае такие вершины в искомом дереве окажутся изолированными, и, следовательно, дерево не будет являться покрывающим.
2. Общее количество ребер в минимальном покрывающем дереве должно быть в точности равно 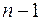 , где
, где 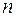 – общее количество вершин исходного графа. Действительно, если некоторое дерево содержит меньше
– общее количество вершин исходного графа. Действительно, если некоторое дерево содержит меньше 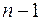 ребер, то оно не будет покрывающим, если же дерево содержит более
ребер, то оно не будет покрывающим, если же дерево содержит более 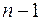 ребер, то оно будет содержать цикл.
ребер, то оно будет содержать цикл.
Введем в рассмотрение 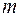 булевых переменных, которые для удобства обозначаются через
булевых переменных, которые для удобства обозначаются через 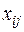 и интерпретируются следующим образом. Переменная
и интерпретируются следующим образом. Переменная 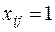 , если ребро
, если ребро 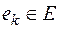 , которому соответствует пара вершин
, которому соответствует пара вершин 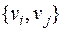 , входит в искомое покрывающее дерево минимальной стоимости, и
, входит в искомое покрывающее дерево минимальной стоимости, и 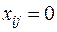 , в противном случае, т.е. если ребро
, в противном случае, т.е. если ребро 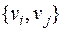 не входит в оптимальное покрывающее дерево. Заметим, что количество рассматриваемых булевых переменных конечно и равно
не входит в оптимальное покрывающее дерево. Заметим, что количество рассматриваемых булевых переменных конечно и равно 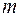 , где
, где 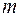 – количество ребер исходного графа.
– количество ребер исходного графа.
Тогда математическая постановка задачи о минимальном покрывающем дереве в графе может быть сформулирована следующим образом.
Найти минимум целевой функции
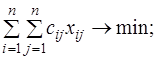 (4)
(4)
при ограничениях
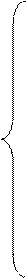
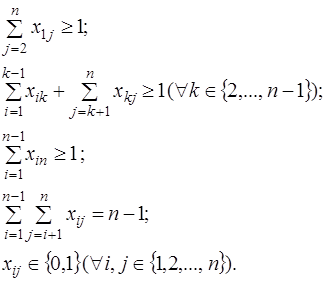 (5)
(5)
Первые три ограничения в системе ограничений (5) требуют выполнения первого из отмеченных ранее свойств, т.е. в искомом покрывающем дереве не должно быть изолированных вершин. Четвертое ограничение в (5) требует выполнения второго из отмеченных ранее свойств, т.е. искомое покрывающее дерево должно содержать ровно 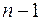 ребер. Наконец, последнее ограничение в (5) требует, чтобы переменные принимали только булевы значения.
ребер. Наконец, последнее ограничение в (5) требует, чтобы переменные принимали только булевы значения.
Примечание: В исходном графе рассматриваемой задачи не должно быть висячих вершин. Для того чтобы минимальное покрывающее дерево было связным и не имело циклов необходимо указать в качестве ограничений для ребер, связывающих эти вершины, значения 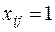 .
.
 2015-06-24
2015-06-24 361
361








