Решение. Для рассматриваемого примера математическая постановка задачи о минимальном покрывающем дереве может быть записана в следующем виде

Для рассматриваемого примера математическая постановка задачи о минимальном покрывающем дереве может быть записана в следующем виде:

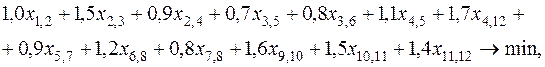(3)

где множество допустимых альтернатив формируется следующей системой ограничений:

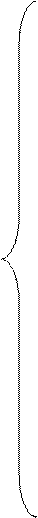
(4)

Для решения данной задачи с помощью программы MS Excel создадим новую книгу и изменим имя ее первого листа на Покрывающее дерево. Для решения поставленной задачи выполним следующие подготовительные действия.

1. Внесем необходимые надписи в ячейки A1:F1, A11 (рис. 7). Следует отметить, что конкретное содержание этих надписей не оказывает влияние на решение рассматриваемой задачи.

2. В ячейки A2:A14 введем индексы начальных вершин, а в ячейки B2:B14 – индексы конечных вершин всех имеющихся ребер исходного графа.

3. В ячейки C2:C14 введем значения коэффициентов целевой функции (1).

4. В ячейку F2 введем формулу: =СУММПРОИЗВ(C2:C14; D2:D14), которая представляет собой целевую функцию (3).

5. В ячейки E2:E13 введем значение левых частей первых двенадцати ограничений системы ограничений (4) (см. рис. 7).

6. В ячейку D15 введем формулу: =СУММ(D2:D14), которая представляет собой левую часть тринадцатого ограничения в системе (4).

Внешний вид рабочего листа MS Excel с исходными данными решения задачи о минимальном покрывающем дереве в графе имеет вид, представленный на рис. 7.

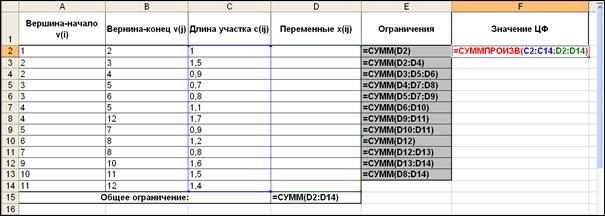
Рис. 7. Исходные данные для решения задачи о минимальном

покрывающем дереве в графе

Далее следует вызвать мастер поиска решения, для чего необходимо выполнить операцию главного меню Сервис→Поиск решения.

После появления диалогового окна Поиск решения следует выполнить следующие действия:

1. В поле с именем Установить целевую ячейку: ввести абсолютный адрес ячейки $F$2.

2. Для группы Равной: выбрать вариант поиска решения – минимальному значению.

3. В поле с именем Изменяя ячейки: ввести абсолютный адрес ячеек $D$2:$D$14.

4. Задать ограничения рассматриваемой задачи, как показано на рис. 8.

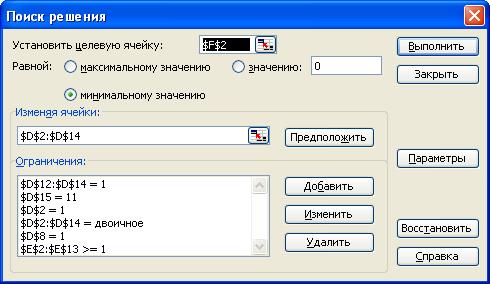
Рис. 8. Переменные и параметры поиска решения

Примечание – В исходном графе рассматриваемой задачи не должно быть висячих вершин. В данном случае имеются висячие вершины – это вершины с номерами 1, 9, 10, 11 и 12. Для того чтобы минимальное покрывающее дерево было связным и не имело циклов необходимо указать в качестве ограничений для ребер, связывающих эти вершины, значения 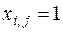, т.е. $D$2=1, $D$8=1, $D$12:$D$14=1 (см. рис. 8).

5. В окне дополнительных параметров поиска решения выбрать отметки Линейная модель и Неотрицательные значения.

После задания ограничений и целевой функции можно приступить к поиску численного решения. После выполнения расчетов программой MS Excel будет получено количественное решение, представленное на рис. 9.

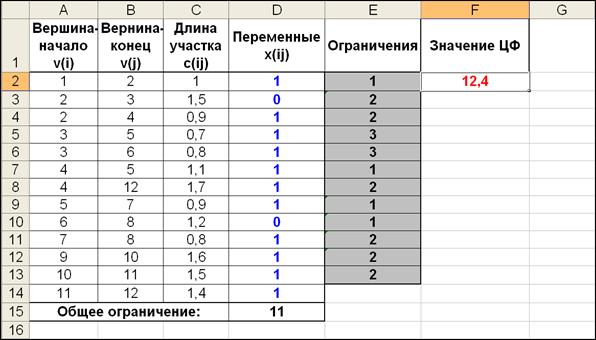
Рис. 9. Результат решения задачи о минимальном покрывающем дереве в графе

Результатом решения задачи о минимальном покрывающем дереве в графе являются найденные оптимальные значения переменных: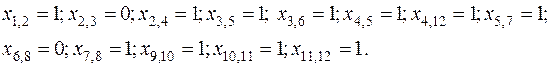

Найденному оптимальному решению соответствует значение целевой функции: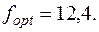

На рис. 10 представлено минимальное покрывающее дерево исходного графа.

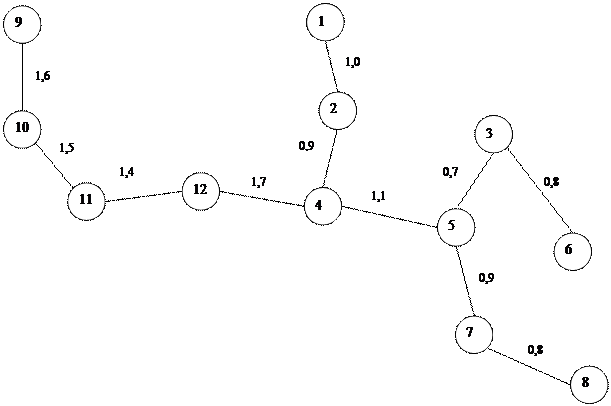
Рис. 10. Минимальное покрывающее дерево исходного графа

Вывод. Найден оптимальный проект транспортной сети, связывающей по кратчайшему расстоянию все микрорайоны города. Суммарная протяженность всех автодорог, по которым пройдут автобусные маршруты, минимальна и составляет 12,4 км.