2015-06-24
486
Решить задачу о минимальном покрывающем дереве в графе, используя в качестве исходных данных граф транспортных связей микрорайонов города, представленный на рис. 6, и матрицу смежности исходного графа, представленную в табл. 2.
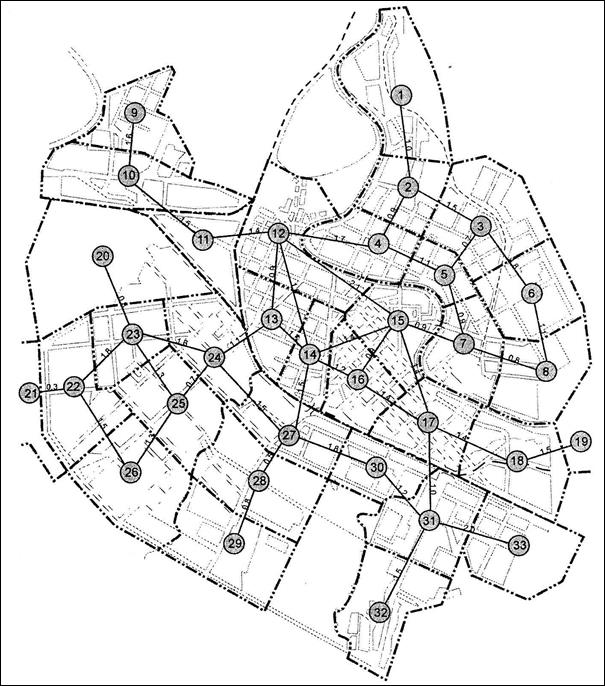
Рис. 6. Граф транспортных связей микрорайонов города
Таблица 2
Матрица смежности исходного графа
| v1 | v2 | v3 | v4 | v5 | v6 | v7 | v8 | v9 | v10 | v11 | v12 | v13 | v14 | v15 | v16 | v17 | v18 | v19 | v20 | v21 | v22 | v23 | v24 | v25 | v26 | v27 | v28 | v29 | v30 | v31 | v32 | v33 | |
| v1 | 1,0 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | |
| v2 | 1,5 | 0,9 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ||
| v3 | ∞ | 0,7 | 0,8 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | |||
| v4 | 1,1 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | 1,7 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ||||
| v5 | ∞ | 0,9 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | |||||
| v6 | ∞ | 1,2 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ||||||
| v7 | 0,8 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | 0,9 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | |||||||
| v8 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ||||||||
| v9 | 1,6 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | |||||||||
| v10 | 1,5 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ||||||||||
| v11 | 1,4 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | |||||||||||
| v12 | 0,9 | 1,6 | 2,1 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ||||||||||||
| v13 | 1,5 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | 1,1 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | |||||||||||||
| v14 | 1,4 | 1,2 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | 1,5 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ||||||||||||||
| v15 | 0,9 | 1,4 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | |||||||||||||||
| v16 | 1,4 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ||||||||||||||||
| v17 | 1,4 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | 1,0 | ∞ | ∞ | |||||||||||||||||
| v18 | 1,5 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ||||||||||||||||||
| v19 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | |||||||||||||||||||
| v20 | ∞ | ∞ | 0,8 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ||||||||||||||||||||
| v21 | 0,3 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | |||||||||||||||||||||
| v22 | 1,8 | ∞ | ∞ | 1,5 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ||||||||||||||||||||||
| v23 | 1,6 | 1,3 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | |||||||||||||||||||||||
| v24 | 0,7 | ∞ | 1,5 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ||||||||||||||||||||||||
| v25 | 1,3 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | |||||||||||||||||||||||||
| v26 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ||||||||||||||||||||||||||
| v27 | 0,5 | ∞ | 1,8 | ∞ | ∞ | ∞ | |||||||||||||||||||||||||||
| v28 | 0,8 | ∞ | ∞ | ∞ | ∞ | ||||||||||||||||||||||||||||
| v29 | ∞ | ∞ | ∞ | ∞ | |||||||||||||||||||||||||||||
| v30 | 1,2 | ∞ | ∞ | ||||||||||||||||||||||||||||||
| v31 | 1,5 | 2,0 | |||||||||||||||||||||||||||||||
| v32 | ∞ | ||||||||||||||||||||||||||||||||
| v33 |
Примечание: Матрица смежности является симметричной, т.е. расстояния между пунктами в прямом и обратном направлении равны. Знак «∞» означает отсутствие прямой связи между пунктами.
Пример выполнения задания
Рассчитать кратчайшую транспортную сеть, использую в качестве исходных данных первые 12 пунктов графа транспортных связей микрорайонов города, представленного на рис. 6, и матрицы смежности исходного графа, представленной в табл. 2.
