Степенно и ее основные свойства:
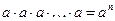 , где
, где 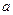 -основание степени,
-основание степени, 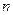 - показатель степени.
- показатель степени.
1) 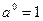 ;
;
2) 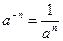 ;
;
Если 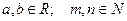 , то:
, то:
3) 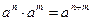 ;
;
4) 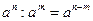 ;
;
5) 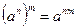 ;
;
6) 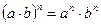 ;
;
7) 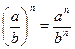 .
.
Арифметический корень и его основные свойства:
Если 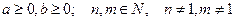 , то
, то
1) 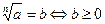 и
и 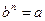 ;
;
2) 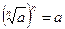 ;
;
3) 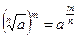 ;
;
4) 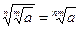 ;
;
5) 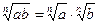 ;
;
6) 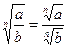 .
.
Абсолютная величина и её основные свойства:
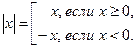
1) 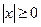 ;
;
2) 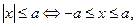 где
где 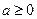 ;
;
3) 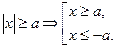
4) 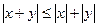 ;
;
5) 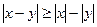 ;
;
6) 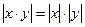 ;
;
7) 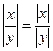 , где
, где 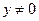 .
.
Формулы сокращенного умножения:
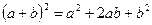 -квадрат суммы;
-квадрат суммы;
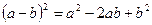 -квадрат разности;
-квадрат разности;
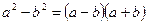 - разность квадратов;
- разность квадратов;
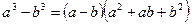 - разность кубов;
- разность кубов;
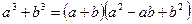 - сумма кубов;
- сумма кубов;
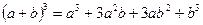 - куб суммы;
- куб суммы;
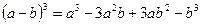 - куб разности;
- куб разности;
Решение квадратного уравнения 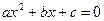 :
:
1) 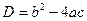 ;
; 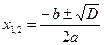 .
.
2) Если квадратное уравнение приведенное, т.е. 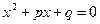 , то корни можно найти по
, то корни можно найти по
теореме Виета: 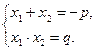
Дли разложения квадратного трехчлена на множители можно использовать теорему:
Если 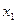 и
и 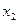 - корни квадратного уравнения
- корни квадратного уравнения 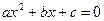 , то
, то 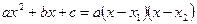 .
.
Логарифм и его свойства:
Определение: 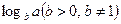 называется показатель степени в которую нужно возвести число
называется показатель степени в которую нужно возвести число 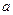 , чтобы получить число
, чтобы получить число 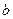 , т.е.
, т.е. 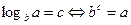 .
.
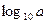 называют десятичным и обозначают
называют десятичным и обозначают  .
.
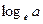 называют натуральным и обозначают
называют натуральным и обозначают 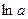 .
.
Свойства логарифмов:
1) 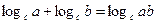 ,где
,где 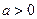 и
и 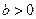 .
.
2) 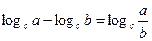 , где
, где 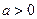 и
и 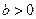 .
.
3) 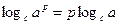 , где
, где 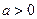 .
.
4) 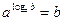 - основное логарифмическое тождество, где
- основное логарифмическое тождество, где 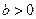 .
.
 2015-06-24
2015-06-24 166
166







