п.2. Вычисление несобственных интегралов

а) интегралы вида .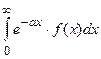

Если f (x) удовлетворяет условиям оригинала, то можно воспользоваться интегралом Лапласа 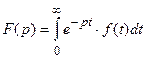, где p = a, тогда

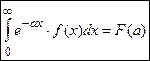
Пример. Вычислить интеграл .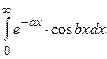

В данном случае f (x) = cos bx, по таблице найдем его изображение

.

.

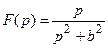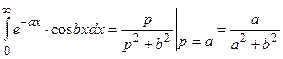(В мат. анализе этот интеграл мы вычисляли дважды по частям.)

б) интегралы вида .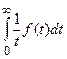

По следствию из теоремы об интегрировании изображения

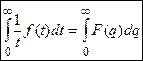
Пример. Вычислить 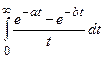, a > 0, b > 0.

.

.

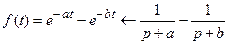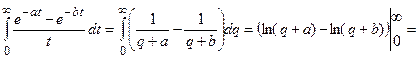
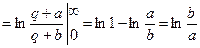в) интегралы вида .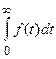

Этот интеграл является частным случаем для интегралов из пункта а) при а = 0, поэтому

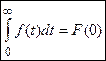
Пример. В §3 было показано, что

.

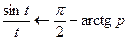Тогда

.

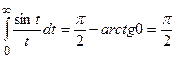(Первообразная для этой функции не существует, такой интеграл по формуле Ньютона-Лейбница не вычисляется.)