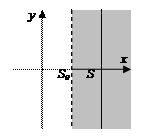
 Отображение, обратное к отображению Лапласа называется отображением Меллина
Отображение, обратное к отображению Лапласа называется отображением Меллина
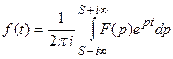 ,
,
где интегрирование ведется по любой прямой Re p = S, S > S 0.
Непосредственное применение формулы обращения часто затруднительно и обычно пользуются теоремами разложения, являющимися следствиями из нее.
Первая теорема разложения. Если функция F (p) аналитична в окрестности бесконечно удаленной точки и ее разложение в ряд Лорана имеет вид
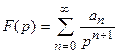 ,
,
то оригиналом является функция
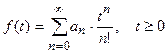 .
.
Вторая теорема разложения. Если F (p) имеет конечное число особых точек p 1, p 2,..., pn, то
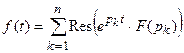 .
.
Во многих случаях оригинал легко восстанавливается по таблице изображений и свойствам преобразования Лапласа.
Пример 1. Найти оригинал для функции 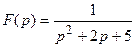 .
.
Преобразуем функцию, выделив в знаменателе полный квадрат.

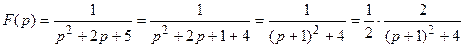 .
.
По таблице найдем оригинал
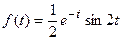 .
.
Пример 2. Найти оригинал для функции 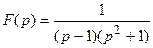 .
.
1 способ. Представим дробь в виде суммы простейших дробей
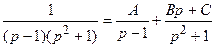 .
.
Вычислив неопределенные коэффициенты, получим
 .
.
Для каждой дроби можно найти оригинал по таблице:
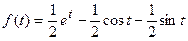 .
.
2 способ. Воспользуемся второй теоремой разложения.
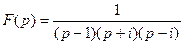
Функция имеет три особые точки p 1 = 1, p 2 = i, p 3 = – i, являющиеся полюсами первого порядка. Найдем вычеты в этих точках для функции eptF (p):
Res(eptF (p), p 1) = 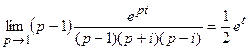 ,
,
Res(eptF (p), p 2) = 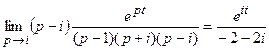 ,
,
Res(eptF (p), p 3) = 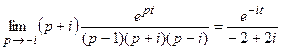 .
.
Оригинал является суммой вычетов:
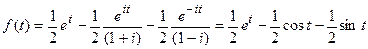 .
.
Пример 3. Найти оригинал для функции 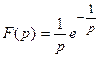 .
.
Воспользуемся первой теоремой разложения. Запишем ряд Лорана для функции F (p) в окрестности точки 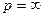 по известному разложению для экспоненты:
по известному разложению для экспоненты:
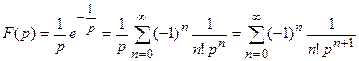 .
.
Оригинал:
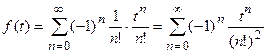 .
.
 2015-06-24
2015-06-24 6920
6920