2015-06-24
492
Проверим выполняются ли свойства у бинарного отношения r заданного на множестве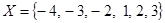 
, если известно, что xry тогда и только тогда, когда 
.
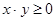Таким образом,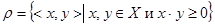 
.
1) Рефлексивность: для любого x Î X выполняется xrx
для любого x Î X выполняется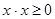 
, значит рефлексивность выполняется.
2) Симметричность: для любых x, y Î X из xry следует yr x
для любых x, y Î X из 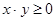следует 
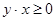, так как умножение чисел коммутативно, значит симметричность выполняется.
3) Транзитивность: для любых x, y, z Î X из xry и yrz следует xrz
так как x, y, z Î X и выполняются неравенства 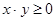и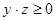 
, значит x, y, z – это числа либо одновременно отрицательные, а произведение отрицательных чисел всегда больше нуля, либо одновременно неотрицательные, тогда выполняется неравенство 
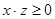, значит свойство транзитивности выполняется.
4) 
Так как выполняются свойства рефлексивности, симметричности и транзитивности, то бинарное отношение r обладает свойством эквивалентности.
Класс эквивалентности порожденный -4, состоит из чисел -4, -3, -2: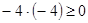 
, 
, 
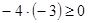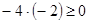, т.е 
.
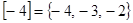Ясно, что этот же класс порождается -3 и -2: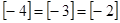 
.
Класс эквивалентности порожденный 1, состоит из 1, 2, 3: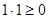 
, 
, 
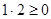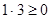, т.е. 
.
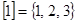Ясно, что этот же класс порождается 2 и 3: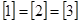 
.
Таким образом, это бинарное отношение r «быть одного знака». Множество X можно разбить на два класса – отрицательные и положительные числа.
5) Антисимметричность: для любых x, y Î X из xry и yrx следует x=y.
существуют такие х и у, что есл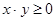и и 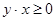,то при этом 
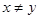, например, 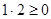и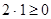 
, но при этом 
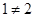, значит свойство антисимметричности не выполняется.
6) Так как выполняются свойства рефлексивности и транзитивности, но не выполняется свойство антисимметричности, то бинарное отношение r не обладает свойством частичного порядка.
