Содержание. п. 1.1. Функциональное уравнение линейной однородной функции

Введение 2

§1. Уравнения Коши. 5

п. 1.1. Функциональное уравнение линейной однородной функции. 5

п. 1.1.1 Класс непрерывных функций. 6

п. 1.1.2 Класс монотонных функций. 7

п. 1.1.3 Класс ограниченных функций. 8

п.1.1.4. Класс дифференцируемых функций. 10

п.1.2. Функциональное уравнение показательной функции. 11

п.1.3. Функциональное уравнение логарифмической функции. 12

п.1.4. Функциональное уравнение степенной функции. 13

п.1.5. Одно обобщение уравнения Коши. 14

§ 2. Метод сведения функционального уравнения к известному уравнению с помощью замены переменной и функции. 17

§ 4. Решение функциональных уравнений с применением теории групп. 24

§ 5. Применение теории матриц к решению функциональных уравнений. 28

§ 6. Применение элементов математического анализа к решению функциональных уравнений. 34

п 6.1. Предельный переход. 34

п. 6.2. Дифференцирование 39

Заключение 42

Список литературы. 43

Введение

Функциональное уравнение - это уравнение, в котором неизвестными являются функции (одна или несколько). Например,

f(x)+xf(x+1) = 1

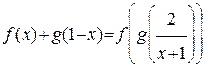
Некоторые функциональные уравнения знакомы нам еще из школьного курса это f(x) = f(-x), f(-x) = - f(x), f(x+T) = f(x), которые задают такие свойства функций, как чётность, нечётность, периодичность.

Задача решения функциональных уравнений является одной из самых старых в математическом анализе. Они появились почти одновременно с зачатками теории функций. Первый настоящий расцвет этой дисциплины связан с проблемой параллелограмма сил. Ещё в 1769 году Даламбер свёл обоснование закона сложения сил к решению функционального уравнения

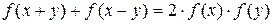(1)

То же уравнение и с той же целью было рассмотрено Пуассоном в 1804 году при некотором предположении аналитичности, между тем как в 1821 году Коши (1789 – 1857) нашёл общие решения

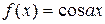
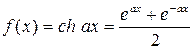
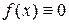
этого уравнения, предполагая только непрерывность f(x).

Даже известная формула неевклидовой геометрии для угла параллельности

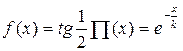
была получена Н. И. Лобачевским (1792 – 1856) из функционального уравнения

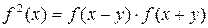, (2)

которое он решил методом, аналогичным методу Коши. Это уравнение можно привести к уравнению

.

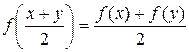Ряд геометрических задач, приводящих к функциональным уравнениям, рассматривал английский математик Ч. Баббедж (1792—1871). Он изучал, например, периодические кривые второго порядка, определяемые следующим свойством для любой пары точек кривой: если абсцисса второй точки равна ординате первой, то ордината второй точки равна абсциссе первой. Пусть такая кривая является графиком функции у = f(х); (х, f(х)) — произвольная ее точка. Тогда, согласно условию, точка с абсциссой f(х) имеет ординату х. Следовательно,

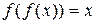(3)

Функциональному уравнению (3) удовлетворяют, в частности, функции:

,

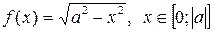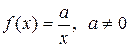
Одними из простейших функциональных уравнений являются уравнения Коши

f(x+y) = f(x)+f(y), (4)

f(x+y) = f(x)·f(y), (5)

f(xy) = f(x)+f(y), (6)

f(xy) = f(x)·f(y), (7)

Эти уравнения Коши подробно изучил в своём (Курсе Анализа), изданном в 1821 году. Непрерывные решения этих четырёх основных уравнений имеют соответственно вид

, , ,

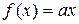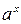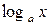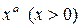
В классе разрывных функций могут быть и другие решения. Уравнение (4) ранее рассматривалось Лежандром и Гауссом при выводе основной теоремы проективной геометрии и при исследовании гауссовского закона распределения вероятностей.

Функциональное уравнение (4) было опять применено Г. Дарбу к проблеме параллелограмма сил и к основной теореме проективной геометрии; его главное достижение - значительное ослабление предположений. Мы знаем, что функциональное уравнение Коши (4) характеризует в классе непрерывных функций линейную однородную функцию f(x) = ax. Дарбу же показал, что всякое решение, непрерывное хотя бы в одной точке или же ограниченное сверху (или снизу) в произвольно малом интервале, также должно иметь вид f(x) = ax. Дальнейшие результаты по ослаблению предположений следовали быстро один за другим (интегрируемость, измеримость на множестве положительной меры и даже мажорируемость измеримой функцией). Возникает вопрос: существует ли хоть одна какая-нибудь аддитивная функция (т. е. удовлетворяющая (4)), отличная от линейной однородной. Найти такую функцию действительно нелегко! В ходе работы мы покажем, что при рациональных x значения любой аддитивной функции должны совпадать со значениями некоторой линейной однородной функции, т. е. f(x) = ax для x 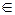Q. Казалось бы, что тогда f(x) = ax для всех действительных x. Если f(x) - непрерывна, то это действительно так, если же данное предположение отбросить - то нет. Первый пример отличного от f(x) = ax разрывного решения функционального уравнения (4) построил в 1905 году немецкий математик Г. Гамель с помощью введённого им базиса действительных чисел.

Многие функциональные уравнения не определяют конкретную функцию, а задают широкий класс функций, т. е. выражают свойство, характеризующее тот или иной класс функций. Например, функциональное уравнение f(x+1) = f(x) характеризует класс функций, имеющих период 1, а уравнение f(1+x) = f(1-x) - класс функций, симметричных относительно прямой x = 1, и т. д.

Вообще, для функциональных уравнений, не сводящихся к дифференциальным или интегральным, известно мало общих методов решения. Далее будут рассмотрены некоторые приёмы, позволяющие решать функциональные уравнения.