2.1.Основные понятия:
- Если 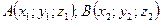 , то
, то 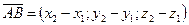 ;
;
- Если 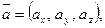 то
то 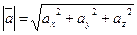 - длина вектора и
- длина вектора и 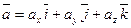 - разложение вектора по ортам координатных осей;
- разложение вектора по ортам координатных осей;
- 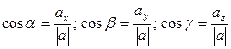 - направляющие косинусы вектора
- направляющие косинусы вектора 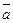 , где
, где 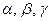 - углы, образованные вектором
- углы, образованные вектором 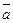 и координатными осями,
и координатными осями, 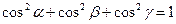 .
.
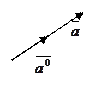
-

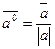 - орт вектора
- орт вектора 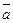
2.2. Скалярное произведение векторов:
Определение:
Скалярным произведением двух ненулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними.
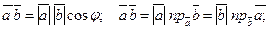
Свойства: Приложения: 1) 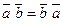 1)
1) 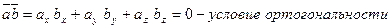
2) 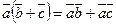 2)
2) 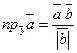 ;
; 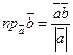
 3)
3) 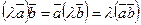 3)
3) 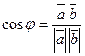
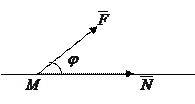 4)
4) 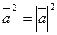 4)
4) 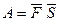
5) 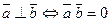
2.3. Векторное произведение векторов:
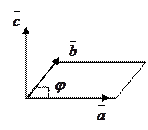 Определение:
Определение:
Векторным произведением двух ненулевых векторов, называется третий вектор 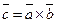 , который удовлетворяет условиям:
, который удовлетворяет условиям:
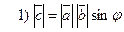 ;
;
2) 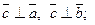
3) 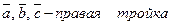 .
.
Свойства: Приложения:
1) 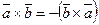 1)
1) 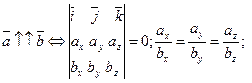
2) 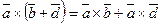 2)
2) 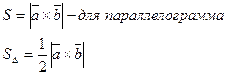

3) 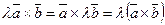 3)
3) 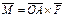 - момент силы
- момент силы 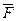 ,
,
приложненной к точке А,
относительно точки О.
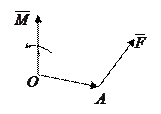
4) 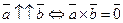
4) 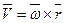 - линейная скорость
- линейная скорость 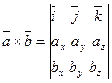 - формула вычисления вращения.
- формула вычисления вращения.
2.4. Смешанное произведение векторов:
Определение:
Смешенным произведением трех ненулевых векторов 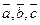 называется произведение, в котором два первых вектора перемножаются векторно, а их результат скалярно на третий вектор.
называется произведение, в котором два первых вектора перемножаются векторно, а их результат скалярно на третий вектор.
1) 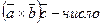
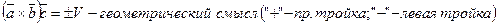
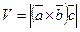 - объем параллелепипеда.
- объем параллелепипеда.
Свойства смешанного произведения:
2) 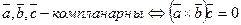
3) 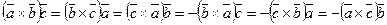
4) 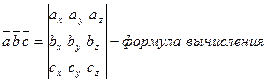 , где
, где 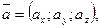
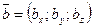 ,
, 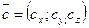
5) Приложения:
- 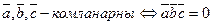
- 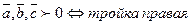 ;
; 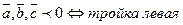
- 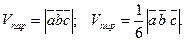
 2015-06-26
2015-06-26 354
354








