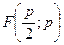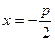Раздел III: аналитическая геометрия

3.1. Задачи на точку:

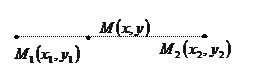1) 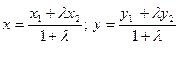-деление отрезка в

заданном отношении ;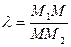

2) Если 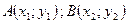, то 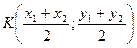- середина отрезка;

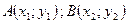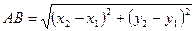3) Если , то - расстояние между точками А

и В.

3.2. Связь прямоугольной и полярной систем координат:

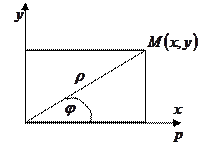
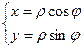-прямоугольные координаты через полярные;

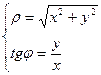-полярные координаты через прямоугольные, где

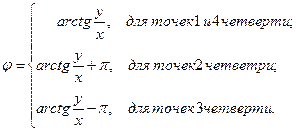
3.3. Виды уравнений прямой на плоскости:

1) 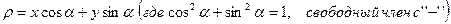- нормальное уравнение прямой,

2) 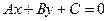- общее уравнение прямой, где 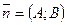- нормальный вектор,

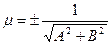нормирующий множитель для сведения общего уравнения к нормальному

3) 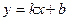- уравнение с угловым коэффициентом (b-ордината точки пересечения с oy)

4) 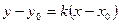- уравнение пучка прямых;

5) 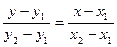- уравнение прямой, проходящей через 2 точки с кордитами

;

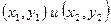6) 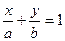- уравнение прямой в отрезках;

3.4. Задачи на прямую на плоскости:

1) 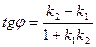- угол между прямыми с угловыми коэффициентами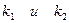

2) 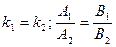- условие параллельности прямых;

3) 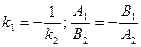- условие перпендикулярности прямых;

4) 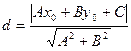- расстояние от 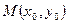до прямой Ах+Ву+С=0.

3.5. Уравнения окружности:

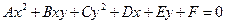- общее уравнение кривой второго порядка.

Определение: Окружностью называется ГМТ плоскости, равноудаленных от одной и той же точки, называемой центром, на одно и то же расстояние, называемое радиусом.

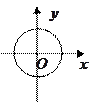
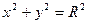- каноническое уравнение окружности;

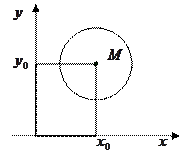
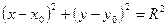- уравнение окружности с центром 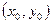и радиусом R

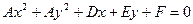- общее уравнение окружности, т.к. коэффициенты при квадратах переменных равны и нет слагаемого, содержащего произведение переменных.

3.6.

Эллипс:

Эллипс – замкнутая кривая, имеющая две взаимно перпендикулярные оси симметрии, называемые осямим эллипса, и центр симметрии, называемый его центром.

Определение:

Эллипсом называется ГМТ плоскости, сумма расстояний от каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная и равная .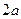

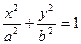-каноническое уравнение эллипса

a

X

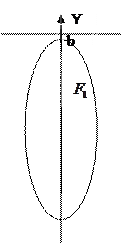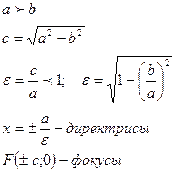
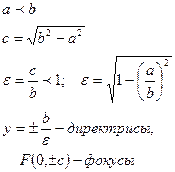
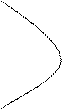
3.7.Парабола:

Определение:

Параболой называется ГМТ плоскости, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой.

Y

X

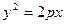-каноническое уравнение параболы

p – расстояние между F и директрисой, характеризует

ширину раствора ее ветвей.

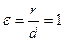
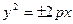- ветви вдоль OX, 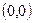- вершина

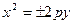- ветви вдоль OY, 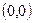- вершина

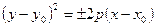- ветви вдоль OX, 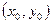- вершина

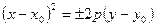- ветви вдоль OY, 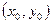- вершина

3.8. Гипербола:

Определение:

Гиперболой называется ГМТ плоскости, разность расстояний от каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная и равная .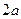

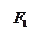
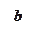
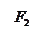
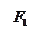
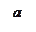
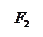
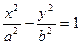
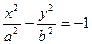
X

b

a

	X

- формула связи - формула связи

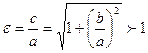
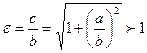
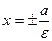- директрисы 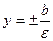- директрисы

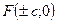
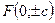
- асимптоты

3.9. Плоскость в пространстве:

1) 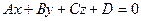- общее уравнение плоскости с нормальным вектором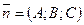

2) 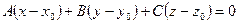- уравнение плоскости проходящей через

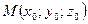и имеющей нормальный вектор .

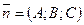3) 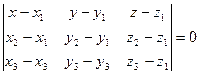- уравнение плоскости, проходящей через точки ; ; .

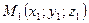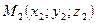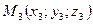4) 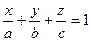- уравнение плоскости в отрезках, где 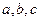- длины отрезков, отсекаемых плоскостью на осях 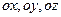соответственно.

3. 10. Задачи на плоскость в пространстве:

Если ,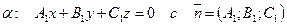

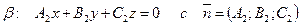, то

1) 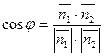- угол между плоскостями;

2) ;

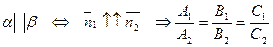3) ;

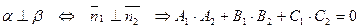4) Если 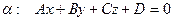, то расстояние от 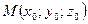до плоскости определяется формулой: .

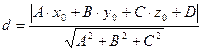3.11. Прямая в пространстве:

1) 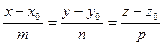- канонические уравнения прямой, проходящей через 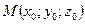с направляющим вектором ;

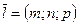2) 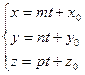- параметрические уравнения прямой;

3) 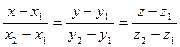- уравнение прямой, проходящей через 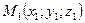и ;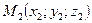

4) 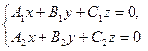- общие уравнения прямой.

Направляющий вектор этой прямой: .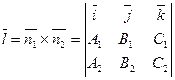

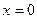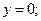Если подставить (или или 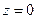) и решить получившуюся систему, то получим одну из точек прямой.

3.12 Задачи на прямую в пространстве:

Если 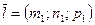- направляющий вектор прямой ,

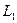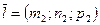- направляющий вектор прямой 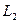, то

1) 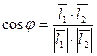- угол между 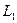и ;

2) ;

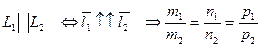3) .

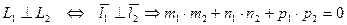3.13 Прямая и плоскость в пространстве:

Если 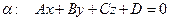с нормальным вектором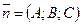

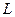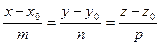: - с направляющим вектором 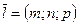,то

1) 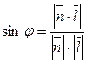- угол между прямой и плоскостью

2)

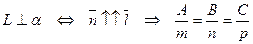
3)

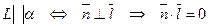
4) Чтобы найти точку пересечения прямой и плоскости:

зададим прямую параметрически, подставим в общее уравнение плоскости, решим

получившееся уравнение относительно 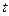, подставим 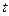в параметрическое уравнение

прямой.