8.1. Определение пределов:
Определение 1:
Число  называется пределом функции
называется пределом функции 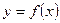 в точке
в точке 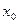 , если для любого положительного
, если для любого положительного 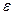 найдется такое положительное
найдется такое положительное 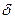 , что для всех
, что для всех 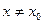 , удовлетворяющих неравенству
, удовлетворяющих неравенству 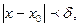 выполняется неравенство
выполняется неравенство 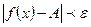
Символически: 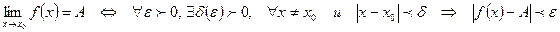
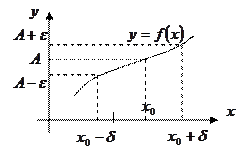
Геометрический смысл: если для 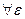 - окрестности т.
- окрестности т.  найдется
найдется 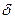 - окрестность
- окрестность 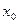 , что для всех
, что для всех 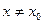 из этой
из этой 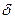 - окрестности соответствующие значения функции
- окрестности соответствующие значения функции  лежат внутри полосы шириной
лежат внутри полосы шириной 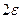 , ограниченной прямыми
, ограниченной прямыми 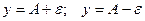 .
.
Определение 2:
Число  называется пределом функции
называется пределом функции 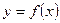 при
при 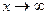 , если для любого
, если для любого 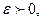 существует
существует 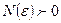 , что при всех
, что при всех  , удовлетворяющих неравенству
, удовлетворяющих неравенству 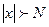 , справедливо неравенство
, справедливо неравенство 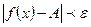 .
.
Обозначение: 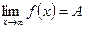 .
.
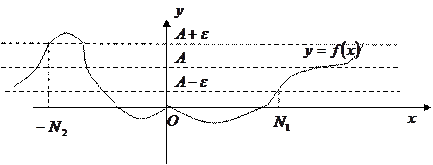 Геометрический смысл: если существует
Геометрический смысл: если существует 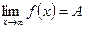 , то для всякого сколь угодно малого наперед заданного числа
, то для всякого сколь угодно малого наперед заданного числа 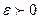 найдется такое свое число
найдется такое свое число 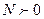 ,
, 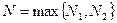 , что, как только становится
, что, как только становится 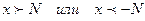 , соответствующие значения функции попадают в
, соответствующие значения функции попадают в 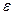 полосу числа
полосу числа  .
.
8.2. БМФ и ББФ:
Определение:
Функция 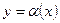 называется бесконечно малой (бмф) при
называется бесконечно малой (бмф) при 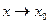 (
(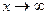 ), если
), если 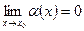 (
(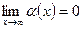 ).
).
Теорема: Сумма конечного числа бесконечно малых функции есть функция бесконечно малая.
Теорема: Произведение бмф на ограниченную (она ограничена в сколь угодно малой окрестности точки) есть функция бесконечно малая.
Следствия:
1) Произведение постоянной на бмф есть бмф;
2) Произведение двух бмф есть бмф;
3) Частное от деления бмф на функцию, имеющую предел, отличный от нуля, есть бмф.
Определение:
Если 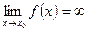
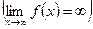 , то
, то  - бесконечно большая функция (ббф).
- бесконечно большая функция (ббф).
Свойства ббф:
1) Произведение ббф на функцию, имеющую предел, отличный от нуля, есть ббф;
2) Произведение двух ббф есть ббф;
3) Сумма и частное двух ббф есть ббф не всегда.
Теорема: Если  - ббф в т.
- ббф в т. 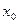 , то
, то 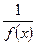 - бмф в т.
- бмф в т. 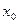 .
.
Теорема: Если 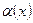 - бмф в т.
- бмф в т. 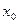 , то
, то 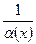 - ббф в т.
- ббф в т. 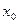 .
.
Теоремы о пределах:
1) Если две функции имеют предел, то их сумма также имеет предел, равный сумме пределов этих функций
2) Если две функции имеют предел, то их произведение также имеет предел, равный произведению пределов этих функций
3) Если две функции имеют предел, то их частное имеет предел, равный частному пределов этих функций, при условии, что предел делителя отличен от нуля.
Следствия:
1) Постоянный множитель можно выносить за знак предела.
2) Теоремы 1и2 остаются справедливыми и в случае любого конечного числа функции, имеющих предел.
8.3. Алгоритм нахождения пределов от алгебраических функций:
1 класс:
Если 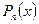 - многочлен
- многочлен  - ой степени, то:
- ой степени, то:
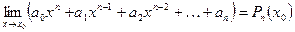 ,
,
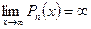 .
.
2 класс:
Если 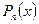 - многочлен
- многочлен  - ой степени,
- ой степени, 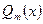 - многочлен
- многочлен 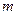 - степени, то
- степени, то
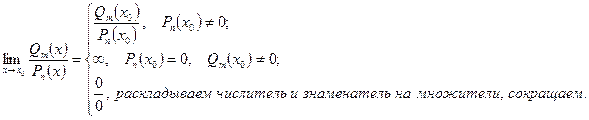
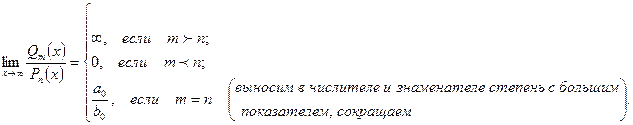
3 класс:
Если 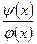 - дробь, содержащая иррациональность, то
- дробь, содержащая иррациональность, то
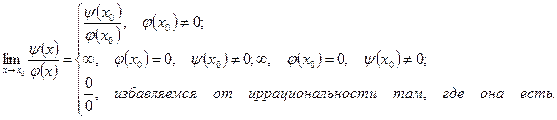
8.4. Замечательные пределы:
1) Теорема:
Предел отношения синуса к его аргументу равен 1, если аргумент стремится к нулю, т.е. 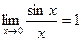 (первый замечательный предел).
(первый замечательный предел).
2) 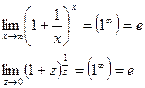 - второй замечательный предел.
- второй замечательный предел.
Следствие: 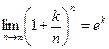 и
и 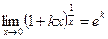 .
.
8.5. Нахождение пределов с использованием бмф:
Пусть 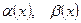 - бмф.
- бмф.
Определение:
Если 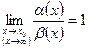 , то
, то 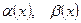 - называются эквивалентными.
- называются эквивалентными.
Обозначение: 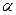 ~
~ 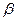
Таблица эквивалентных бмф при 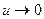 :
:
1) 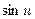 ~
~ 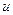 6)
6) 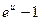 ~
~ 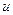
2) 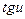 ~
~ 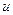
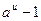 ~
~ 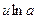
3) 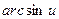 ~
~ 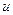 7)
7) 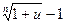 ~
~ 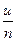
4) 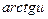 ~
~ 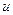 8)
8) 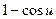 ~
~ 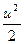
5) 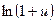 ~
~ 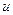
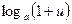 ~
~ 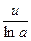
 2015-06-26
2015-06-26 3406
3406








