10.1. Основные понятия:
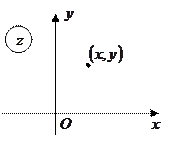
Определение:
Комплексным числом 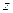 называется упорядоченная пара действительных чисел
называется упорядоченная пара действительных чисел 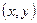 представленная выражением
представленная выражением 
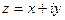 , здесь
, здесь 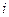 - называют мнимой единицей.
- называют мнимой единицей.
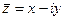 и
и 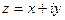 называются комплексно-сопряженными.
называются комплексно-сопряженными.
Комплексное число можно изобразить точкой плоскости 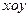 : с координатами
: с координатами 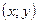 или радиус вектором этой точки.
или радиус вектором этой точки.
Формы записи комплексного числа:
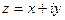 - алгебраическая
- алгебраическая
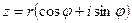 - тригонометрическая
- тригонометрическая
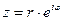 - показательная.
- показательная.
Модуль комплексного числа: 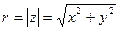 .
.
Основное значение аргумента комплексного числа:
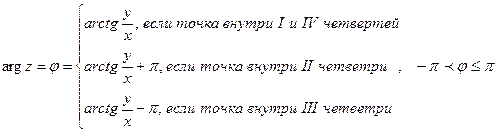
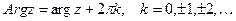 - аргумент комплексного числа.
- аргумент комплексного числа.
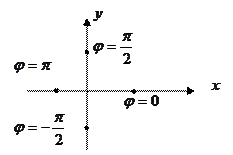
Если комплексное число лежит на одной из координатных осей, то ее главный аргумент находят непосредственно.
10.2. Действия над комплексными числами:
В алгебраической форме:
Если 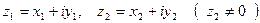 , то
, то
1. 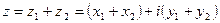 .
.
2. 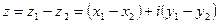 .
.
3. 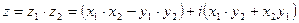 , учитывая
, учитывая 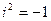 .
.
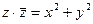 .
.
4. 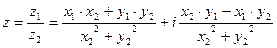 , но чаще
, но чаще 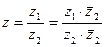 .
.
В тригонометрической и показательной формах:
Если 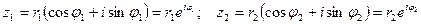 , то
, то
1. 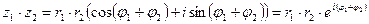 .
.
В частности: 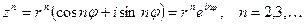
2. 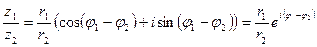 .
.
3. 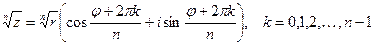 .
.
 2015-06-26
2015-06-26 418
418








