Дифференциальные уравнения равновесия

Предыдущие разделы теории напряжений построены на анализе уравнений равновесия элементов сплошной среды. Это были уравнения первого приближения, которое исчерпывает проблему только в мало интересном случае однородного напряженного состояния, при котором напряжения по объему материала постоянны.

Теория упругости предназначена для исследовании неоднородных напряженных состояний,в которых напряжения являются функциями координат. Напряженное состояние тела описывается шестью скалярными функциями, описывающими распределение по объему среды шести компонентов тензора напряжений

s_x = s_x(x,y,z),

s_y = s_y(x,y,z), (33)

...

t_zx = t_zx(x,y,z).

Исследуем ограничения, накладываемые на эти функции условиями равновесия элемента среды.

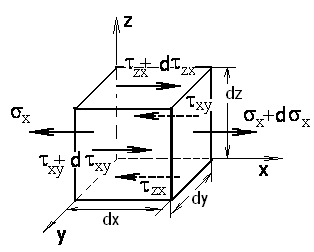
Рис.1.8. Напряжения, проецирующиеся на ось x.

На рис.1.8. изображен элемент среды в форме прямоугольного параллелепипеда со сторонами dx, dy, dz, на гранях которого показаны только те напряжения, которые проецируются на ось х. Составим уравнения равновесия этого элемента в проекциях на ось x.

• На левую грань действует нормальное напряжение s_х, на правую – такое же напряжение с некоторым приращением ds_х. Поскольку при переходе от левой грани к правой получает приращение только координата x, дифференциал s_х может быть записан в виде

ds_х = = .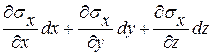

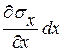• на дальнюю грань действует напряжение t_xy, а на переднюю

t_xy + dt_xy = t_xy + .;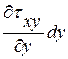

• на нижнюю грань дйствует напряжение t_zx, а на переднюю

t_zx + dt_zx = t_zx + .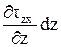

Запищем уравнение равновесия. Просуммируем проекции на ось x сил, действующих на грани элемента. Каждая из сил вычисляется как произведение напряжения на площадь соответствующей грани. Добавим проекцию объемной силы, вычисляя ее как произведение проекции плотности объемной силы X на объем элемента dv = dxdydz. Получим:

-s_хdydz+(s_х+ 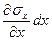)dydz -t_xy dxdz +(t_xy + 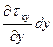)dxdz - t_zxdxdy +(t_zx + 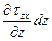)dxdy + Xdxdydz = 0.

После очевидных упрощений, получим

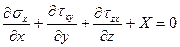
Это и есть дифференциальное уравнение равновесия элемента в проекциях на ось х. Аналогично могут быть получены уравнения равновесия в проекциях на оси y и z. Полностью система дифференциальных уравнений равновесия имеет вид:

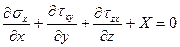
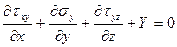(34)

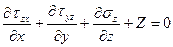
Получим эти уравнения еще раз. Рассмотримм некоторый объем V сплошной среды, ограниченный поверхностью W (рис.1.9), который находится в равновесии под действием поверхностных сил (Sx, Sy, Sz), распределенных по поверхности W и объемных сил (X,Y,Z), распределенных по объему V.

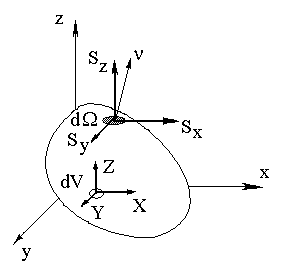
Рис.1.9. Силы, действующие на элемент

поверхности dW и элемент объема dV тела.

Уравнение равновесия тела в поекциях на ось x:

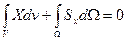(35) Преобразуем второй интеграл. Выразим Sx через напряжения в среде, используя первое уравнение из (6-а),

,

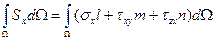где l, m, n – направляющие косинусы площадки dW, а затем преобразуем интеграл поповерхности в интерал по объему:

=

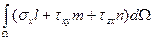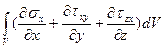
Подставив полученный результат в (35), получим

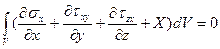(36)

Поскольку в равновесии находится не только все тело объемом V, но и любая его часть, в уравнении (36) в ноль должно обращаться подинтегральное выражение:

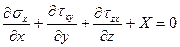
Это –первое дифференциальное уравнение из системы (34). Два другие получаются аналогично из уравнений равновесия в проекциях на оси y и z.