2015-06-26
2678
Пусть известны главные напряжения (s1³ s2 ³s3) и главные площадки. Касательные напряжения на этих площадках равны нулю, а на прочих, неглавных площадках они от нуля отличны. Найдем среди этих площадок такие, на которых касательные напряжения максимальны.
Для этого найдем касательные напряжения на произвольной площадке, направляющие косинусы нормали n к которой обозначим l,m и n. Квадрат полного напряжения на этой площадке определим как сумму квадратов его проекций на главные оси:
(Sn)2 = Sx2+Sy2+Sz2
Применяя к главным осям формулы (6), получим:
(Sn)2 =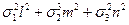 
,
Для определения квадрата нормального напряжения можно воспользоваться первой из формул (9-а):
sn2 = (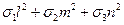
)2 (14)
Тогда квадрат касательного напряжения определится выражением
t2 =(Sn) 2 - sn2 =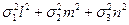 
- (
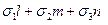)2, (15-а)
или в форме, более удобной для последующих преобразований:
t2 =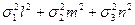 
- sn2. (15-б)
У функции t2 нужно искать экстремум. Задача осложняется тем, что аргументы этой функции – направляющие косинусы l,m и n – взаимозависимы, они связаны условием (11). Для отыскания условного экстремума воспользуемся методом неопределенных множителей Лагранжа [ ], в соответствии с которым экстремум ищется для функции
|
|
|
F(l,m,n)= t2 + l(l2+m2+n2-1),
, где – множитель Лагранжа. Или, с учетом (15-б),
F(l,m,n)= 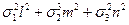- sn2 + l(l2+m2+n2-1), (16)
При выполнении условия (11) экстремумы F совпадают с экстремумами функции t2, но направляющие косинусы в выражении (16) можно рассматривать как независимые.
Дифференцируя F по l,m и n с учетом (14) и приравняв нулю производные, получим три уравнения, выражающие условия экстремальности F или:
2(s12 – 2sns1 + l)l =0 (1)
2(s22 – 2sns2 + l)m =0 (2) (17)
2(s32 – 2sns3 + l)n =0 (3)
Вместе с (11) они составляют систему 4-х уравнений с четырьмя неизвестными l,m,n и l.
Исследуя решения системы уравнений (17)+(11) рассмотрим 4 следующих варианта:
Вариант 1. Все три направляющих косинуса равные нулю всегда удовлетворяет системе (17), но не удовлетворяет уравнению (11), следовательно, решением не является.
Вариант 2. Два направляющих косинуса равны нулю, а третий в соответствии с уравнением (11) равен единице.
Пусть, например, n=1, а l= m =0. В этом случае из (14) получается sn = s3 , первое и второе уравнения из (17) удовлетворяются тождественно, а третье принимает вид s32 –sns3+l=0. оно выполняется при l = s3. Из (15) получаем t2 = 0. Таким наборам направляющих косинусов соответствуют исходные главные площадки, на них касательные напряжения равны нулю, это экстремумы функции t2, но не максимумы, а минимумы.
Вариант 3. Один направляющий косинус равен а два не равны нулю.
Пусть, например, l=0, m≠0, n≠0. Из (14) получим
sn =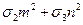 
. (а)
Первое уравнение из(17) удовлетворяется тождественно, а второе и третье приводятся к системе уравнений
|
|
|
s22 – 2sns2 + l = 0 (б)
s32 – 2sns3 + l = 0 (в).
Вычитая (в) из (б), получим
s22 - s32 - 2sn(s2-s3) = 0, откуда
sn =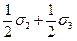 
.
Сравнивая последнее выражение с (а), получаем m2 = n2 =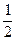 
, т.е m = ± 
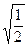, n = ± 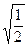. Это решение удовлетворяет уравнению (11) и определяет площадки, на которых касательные напряжения максимальны. Значение касательного напряжения на этих площадках найдем, подставив полученные направляющие косинусы в (15):
t2 =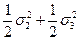 
- 
= 
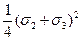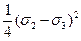или |t|=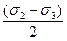 
Найденная площадка перпендикулярна к главной площадке с напряжение s1 и наклонена под углом p/4 к главным площадкам с напряжениями s2 и s3 .
Аналогино можно найти еще два семейства площадок с максимальными касательными напряжениями. Все результаты сведены в таблицу.
| l | m | n | |t| | |
| ±
| ±
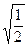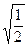| |t|1=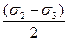 
| ||
| ±
| ±
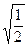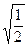| |t|2=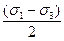 
| ||
| ±
| ±
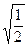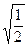| |t|3=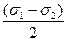 
|
Если главные напряжения пронумерованы в соответствии с традиционным правилом s1 ³ s2 ³ s3, то абсолютному максимуму соответствует напряжение |t|2.
tмах = |t|2 = 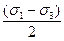(18).
Ориентация площадок, на которых они действуют показана на рис.1.7.
Вариант 4. Все три направляющих косинуса отличны от нуля. Решений нет.
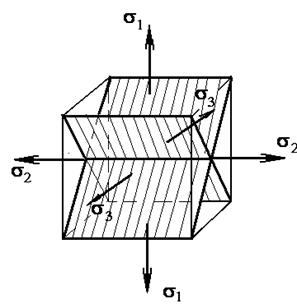
Рис.1.7. Площадки, на которых действуют
максимальные касательные напряжения.
1.8. Инварианты матрицы напряжений.
Вернемся к соотношениям (9), описывающим преобразование компонентов напряжений при повороте координатных осей. Сложим три первых уравнения. Учитывая свойства матрицы (L) (см. (ПР1-....)), получим: sx1 + sy1 + sz1 = sx + sy + sz: сумма нормальных напряжений на трех взаимно перпендикулярных площадках при повороте осей координат остается постоянной.
Комбинации компонентов матрицы, которые не меняются при повороте системы координат называются инвариантами.
Сумма нормальных напряжений на трех взаимно перпендикулярных площадках – один из инвариантов матрицы напряжений.
Инвариантов матрицы напряжений бесконечно много, но только три из них являются независимыми, все остальные могут быть представлены как комбинации выбранных основных или главных инвариантов.
В механике деформируемых тел в качестве главных инвариантов напряжений приняты коэффициенты характеристического уравнения (12).
Первый (линейный) инвариант (он был уже представлен выше), второй (квадратичный) и третий (кубический) инварианты в произвольных осях и в главных осях имеют вид:
I1(s)= А = sx + sy + sz = s1 + s2 + s3,
I2(s)= В = sxsy +sysz +szsx -txy2-tyz2-tzx2 = s1s2 +s2s3 +s3s1 , (19)
I3(s)= С = sxsysz+2txytyztzx–(sxtyz2+sytzx2+sztxy2) = sxsysz.
