Примеры 2 и 3

Пример 2. Балка длиной l прямоугольного поперечного сечения, высотой h, шириной b; жестко закреплена на правом конце, а на левом загружена вертикальной силой P. Используя известное из сопротивления материалов решение технической теории изгиба балок, определить поле напряжений в объеме тела и проверить его соответствие дифференциальным уравнениям равновесия.

Расположим начало координат в центре левого сечения. Ось x совместим с осью балки, а оси y и z с главными осями инерции сечения (рис.1.10).

В произвольном сечении балки с координатой х поперечная сила и изгибающий момент составляют

Q = P, M = - P (l - x).

Нормальные и касательные напряжения в соответствии с учетом принятого здесь обозначения осей и правила знаков:

s = 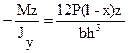= s_x (37-a)

t = 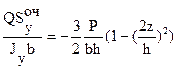= t_zx , (37-б)

где J_y – момент инерции сечения, а S_z^оч – статический момент отчеченной части сечения относительно оси у.

Остальные компоненты тензора напряжений в соответствии с технической теорией изгиба балок равны нулю:

s_y = s_z = t_xy = t_yz = 0, (37-в)

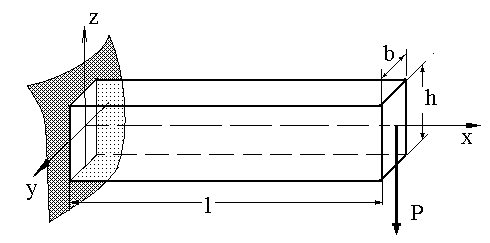
Рис.1.10. К примеру 1.

Проверим уравнения равновесия. По условиям задачи объемные силы отсутствуют: X =Y =Z =0.

Дифференцируя (37-а,б), получим:

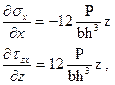
Остальные производные, входящие в уравнения равновесия(30) равны нулю. Полученное поле напряжений дифференциальным уравнениям равновесия удовлетворяет.

Пример 3. Та же самая балка загружена только собственным весом. Плотность материала r, ускорение свободного падения g. Весовая нагрузка, приходящаяся на единицу длины балки q = 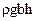. Поперечная сила и изгибающий момент в сечении х составляют:

Q = q(l-x) = 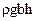(l-x),

M = 0.5 q(l-x)² = ,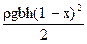

Нормальные и касательные напряжения в поперечном сечении

s_x = s = ,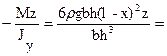

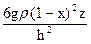t_zx = t = .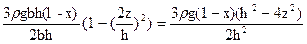

Остальные компоненты напряжений как и в предыдущей задаче равны нулю.

Определим ненулевые производные от напряжений, входящие в уравнения равновесия (30):

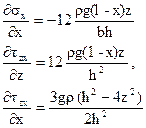(38)

Вес материала является объемной силой, направленной вдоль оси z, дв другие проекции объемной силы равны нулю:

X = 0, Y = 0, Z = -rg.

Подставляя производные (38) и объемные силы в уравнения (34), убеждемся в том, что два первых уравнения удовлетворяются тождественно, а третье (в проекциях на ось z) принимает вид:

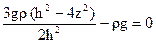. (39)

В произвольной точке (при произвольном z) это уравнение не выполняется. Проинтегрируем его по z от –h/2 до h/2 (по высоте сечения)

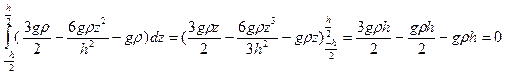
Техническая теория изгиба балок приближенна, ее решения не всегда удовлетворяют более строгим уравнениям теории упругости. В рассматриваемом примере уравнение равновесия в проекциях на ось z удовлетворяется только интегрально, в среднем по высоте сечения.

Замечание. Дифференциальные уравнения равновесия для функций, описывающих напряженное состояние тела, являются необходимыми условиями, но не достаточными. Напряжения должны удовлетворять еще некоторым уравнениям, которые будут получены позже. К анализу этих задач мы еще вернемся.