Теорема 1. 4

Отображение f имеет обратное отображение тогда и только тогда, когда f является инъективным и сюръективным.

Доказательство

Необходимость. Пусть отображение f: A 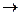B имеет обратное отображение. По определению обратной функции это означает, что в каждый элемент множества B отображение f переводит хотя бы один элемент A. Поэтому f (A) = B, т.е. f - это сюръективное отображение.

Поскольку f ^-1 - отображение, то отображение f переводит в каждый элемент b 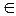B ровно один элемент a 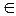A. Следовательно, f - это инъективное отображение.

Достаточность. Пусть отображение f - инъективное и сюръективное. Тогда в каждый элемент b 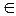B отображение f переводит единственный элемент a 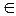A, т.е. f ^-1 является отображением.