Доказательство. Предположим противное. Пусть для некоторого множества A существует взаимно однозначное соответствие элементов этого множества и множества 2A

Предположим противное. Пусть для некоторого множества A существует взаимно однозначное соответствие элементов этого множества и множества 2 ^A .

Обозначим как B_x - множество, соответствующее элементу x Î A.

Рассмотрим множество D = { x | x 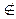B_x }. То есть это все такие элементы из A, которым соответствуют подмножества A, не содержащие эти элементы. Если для некоторого элемента- y 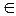A справедливо равенство B_y = Æ, то y 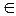D. Следовательно, D ¹ Æ.

Возьмем y 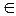A такое что D = B_y.

Возможен лишь один из следующих случаев:

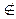а) y B_y;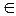

b) y B_y.

В первом случае имеем: если y 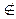B_y, то y 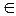D, т.е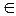. y B_y.

Во втором случае: если y 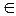B_y, то y 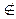D. Поэтому y 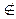B_y, т.е. в обоих случаях получаем противоречие.

Поэтому предположение о существовании взаимно однозначного соответствия между элементами A и 2 ^A является неверным.