№1
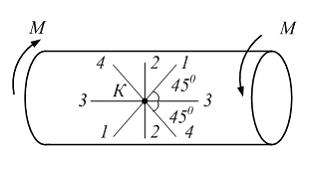
На рисунке показан стержень, работающий на кручение. Максимальное растягивающее напряжение в точке К действует в направлении …
 | 4−4 | ||
| 3−3 | |||
| 1−1 | |||
| 2−2 |
Решение:
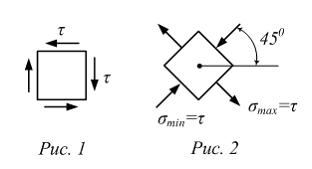
Если в окрестности точки К двумя поперечными, двумя продольно-осевыми и цилиндрическим сечениями выделить элементарный объем, то на его гранях будут действовать касательные напряжения. Напряженное состояние показано на рисунке 1 через плоский элемент. При повороте на угол  касательные напряжения на его гранях исчезают, но появляются нормальные напряжения, показанные на рисунке 2.
касательные напряжения на его гранях исчезают, но появляются нормальные напряжения, показанные на рисунке 2.
№2
Относительный угол закручивания определяется по формуле …
 | 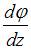 или или 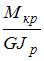 | ||
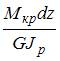 | |||
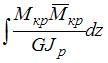 | |||
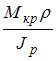 |
Решение:
Выделим из стержня круглого сечения элемент длиной 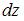 . Предположим, что под действием крутящего момента правое сечение повернется на угол
. Предположим, что под действием крутящего момента правое сечение повернется на угол 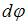 относительно левого.
относительно левого.
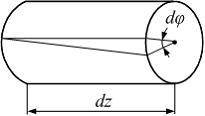
Величина 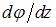 обозначается обычно через
обозначается обычно через 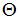
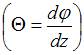
и называется относительным углом закручивания. Это угол взаимного поворота двух сечений, отнесенный к расстоянию между ними.
№3
При кручении стержня круглого поперечного сечения внутренние силы в поперечном сечении приводятся к …
 | моменту относительно оси, перпендикулярной к плоскости сечения и проходящей через его центр тяжести | ||
| моменту относительно главной центральной оси поперечного сечения | |||
| силе, совпадающей с главной центральной осью поперечного сечения | |||
| силе, перпендикулярной к плоскости сечения и проходящей через его центр тяжести |
Решение:
Система внутренних сил в поперечном сечении стержня, на основании положений статики, приводится к центру тяжести сечения. В результате получается главный вектор и главный момент всех внутренних сил. Спроектировав главный вектор и главный момент на оси прямоугольной системы координат, расположенные определенным образом (одна ось направлена по нормали к сечению, а другие расположены в плоскости сечения), получим шесть составляющих: три силы и три момента. Эти составляющие называются внутренними силовыми факторами и имеют определенные наименования. Момент всех внутренних сил относительно оси, перпендикулярной плоскости сечения, называется крутящим моментом. Деформация стержня, когда в поперечном сечении возникает только крутящий момент, называется кручением.
№4
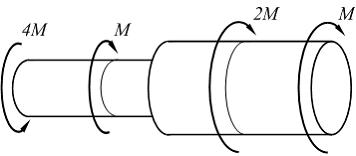
На рисунке показан стержень, работающий на кручение. Крутящий момент на среднем грузовом участке равен …
 | 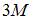 | ||
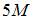 | |||
- 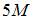 | |||
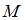 |
Решение:
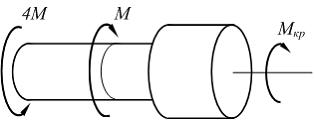
Крутящий момент на среднем грузовом участке определим методом сечений. Разделим стержень на две части произвольным поперечным сечением на среднем участке и рассмотрим равновесие одной из частей (например, левой см. рисунок). Крутящий момент Мкр направляем произвольно. Уравнение равновесия имеет вид 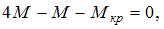 откуда
откуда 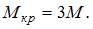
№5
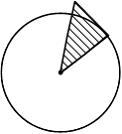
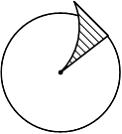
При кручении стержня круглого поперечного сечения касательные напряжения изменяются вдоль радиуса, как показано на рисунке …
 |  | ||
 | |||
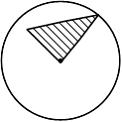 | |||
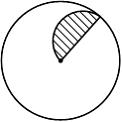 |
Решение:
Формула для касательного напряжения имеет вид 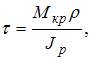 где
где 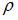 − расстояние от центра тяжести поперечного сечения до точки, в которой определяется напряжение. Зависимость
− расстояние от центра тяжести поперечного сечения до точки, в которой определяется напряжение. Зависимость 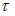 от
от 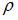 − линейная.
− линейная. 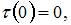
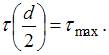
№6
При кручении стержня круглого поперечного сечения напряженное состояние материала во всех точках, за исключением точек на оси стержня, – …
 | чистый сдвиг | ||
| линейное (одноосное растяжение) | |||
| линейное (одноосное сжатие) | |||
| объемное |
Решение:
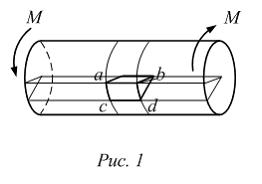
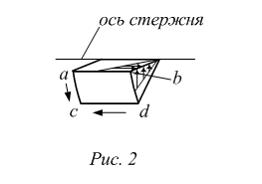
Если из стержня, работающего на кручение (рис. 1), двумя поперечными и двумя продольно-осевыми сечениями вырезать клин (рис. 2), то можно показать, что на его гранях, совпадающих с этими сечениями, действуют только касательные напряжения. Поэтому напряженное состояние материала во всех точках стержня, за исключением точек на оси стержня, – «чистый сдвиг».
№7
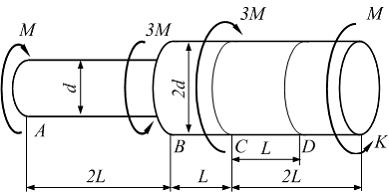
На рисунке показан ступенчатый стержень, работающий на кручение. Величины  заданы. Взаимный угол поворота поперечных сечений A и D равен …
заданы. Взаимный угол поворота поперечных сечений A и D равен …
 | 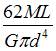 | ||
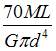 | |||
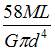 | |||
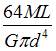 |
Решение:
Методом сечений определяем крутящие моменты на грузовых участках.
На участке 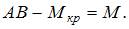
На участке 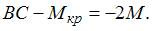
На участке 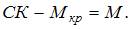
Взаимный угол поворота двух любых сечений равен сумме углов закручивания участков стержня, расположенных между ними. Поэтому 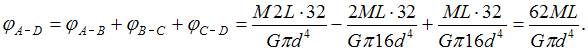
№8
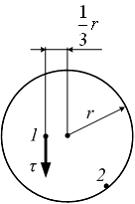
Пусть значение касательного напряжения 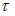 в точке 1 поперечного сечения равно
в точке 1 поперечного сечения равно 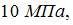 тогда касательное напряжение в точке 2 равно ___ МПа.
тогда касательное напряжение в точке 2 равно ___ МПа.
 | |||
Решение:
При кручении стержня касательные напряжения в точках круглого поперечного сечения определяются по формуле 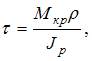 где ρ – расстояние от центра тяжести поперечного сечения до точки, в которой определяется касательное напряжение. Зависимость τ от ρ линейная. Поэтому значение касательного напряжения в точке 2 в три раза больше напряжения в точке 1.
где ρ – расстояние от центра тяжести поперечного сечения до точки, в которой определяется касательное напряжение. Зависимость τ от ρ линейная. Поэтому значение касательного напряжения в точке 2 в три раза больше напряжения в точке 1.
 2015-06-26
2015-06-26 2268
2268