2015-04-12
323
Для дальнейших расчетов нам потребуется эпюра крутящего момента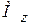 
.
1. Построение эпюры крутящего момента
В заделке А покажем реактивный момент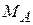 
(рис. 4.6 а). В результате получим систему моментов действующих относительно оси 
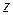, для которой можно составить одно уравнение равновесия. Число неизвестных реакций одно. Таким образом, заданный вал является статически определимым.
|
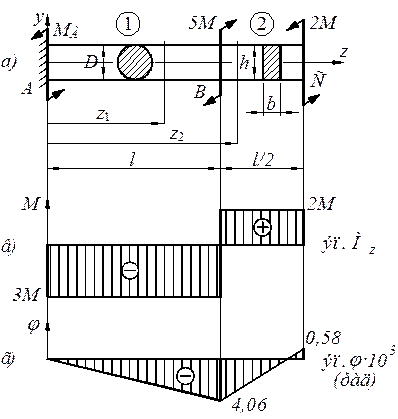
б)
|
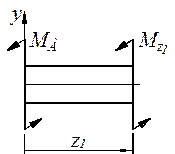
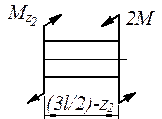
| Рис. 4.5 |
Составим уравнение равновесия и определим :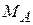
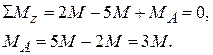
Разбиваем брус на силовые участки – первый (1) и второй (2)
(рис. 4.5 а.)
Используя метод сечений, записываем выражения для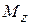 
на каждом силовом участке.
На первом участке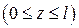 
, (рис. 4.5 б)
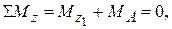
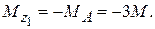(1)
На втором участке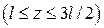 
, (рис. 4.5 б)
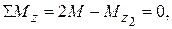
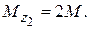(2)
Используя выражения (1), (2), строим эпюру 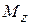(рис. 4.5 в).
2. Определение допускаемого значения крутящих моментов
Из условия прочности вала при кручении
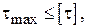(3)
где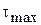 
− максимальное касательное напряжение на одном из участков вала.
На первом участке
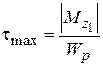, (4)
где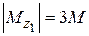 
− крутящий момент на первомучастке; 
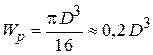− полярный момент сопротивления круглого сечения на первомучастке.
Выражение (4) принимает вид
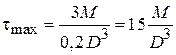. (5)
На втором участке
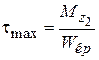, (6)
где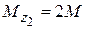 
− крутящий момент на второмучастке;
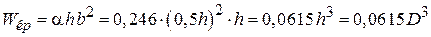− момент сопротивления для прямоугольного поперечного сечения на втором участке, 
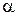− коэффициент, зависящий от отношения 
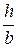и определяемый по таблице, для 
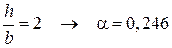. Выражение (6) принимает вид
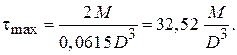(7)
Сравнивая выражения (5) и (7), делаем вывод, что максимальные касательные напряжения будут на втором участке.
Условие прочности (3) можно записать в виде
,
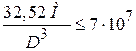откуда с учетом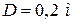 
получим
.
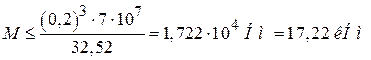Для дальнейших расчетов примем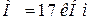 
, тогда
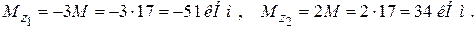
3. Построение эпюры касательных напряжений
Первый участок – круглое поперечное сечение (рис. 4.6).
|
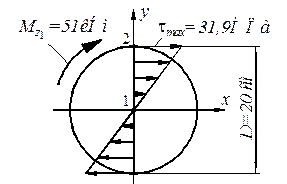
| Рис. 4.6 |
Для построения эпюры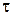 
определим значения касательных напряжений в точках 1 и 2.
В точке 1
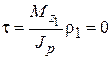, так как 
.
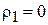В точке 2
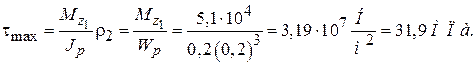
Второй участок – прямоугольное поперечное сечение (рис. 4.7).
|
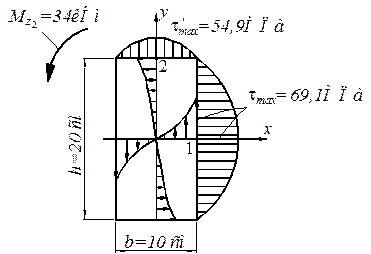
| Рис. 4.7 |
Для построения эпюры 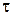рассмотрим точки 1 и 2.
В точке 1
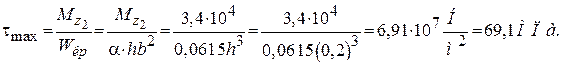
В точке 2
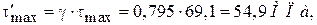
где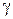 
− коэффициент, зависящий от отношения 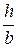и определяемый по таблице, для 
.
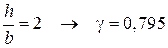4. Построение эпюры углов закручивания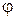 
Для i -го участка, нагруженного постоянным крутящим моментом, угол закручивания можно определить по зависимости
,
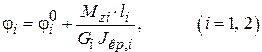где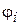 
− угол закручивания на рассматриваемом i -ом участке; 
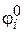− угол закручивания в начале i -ого участка; 
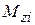− крутящий момент; 
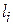− длина участка; 
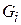− модуль сдвига материала участка; 
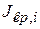− геометрическая характеристика сечения при кручении (для круглого сечения 
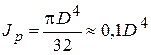, для прямоугольного 
).
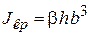В задаче имеем
,
.
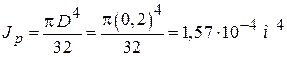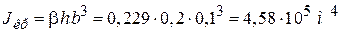На первом участке
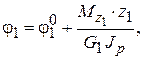(8)
где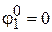 
, так как в начале первогоучастка заделка (точка А); 
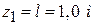− длина первого участка.
Тогда выражение (8) примет вид
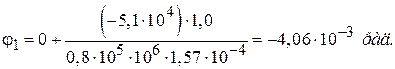
На втором участке
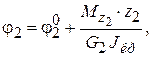(9)
где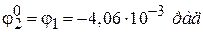 
− угол закручивания в начале второгоучастка (точка B); 
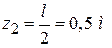− длина второго участка.
Из выражения (9) получим
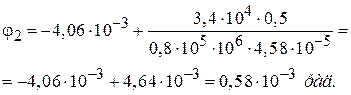
Полученные данные позволяют построить эпюру 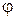(рис. 4.5 г).
№3. Построить эпюру крутящих моментов и угловых перемещений 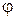, написать условие прочности для стержня, подвергающегося кручению внешними моментами (рис. 4.8).
| а) в) д) e) |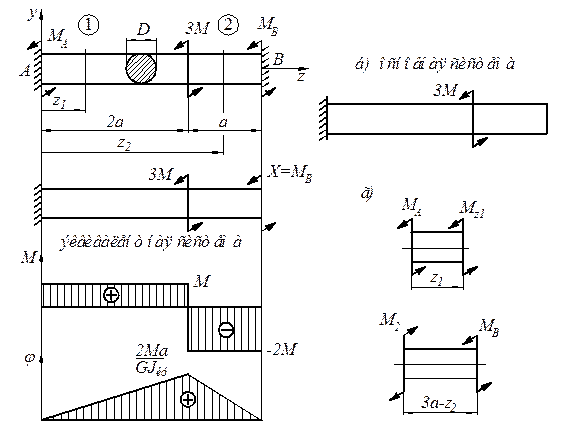 
|
| Рис. 4.8 |
