Рассмотрим стержень круглого поперечного сечения диаметром 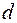 , нагруженного внешним крутящим моментом
, нагруженного внешним крутящим моментом 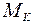 (рис. 5.3). Прямоугольная сетка, нанесенная на его поверхности, после деформации превратится в сетку, состоящую из параллелограммов, что свидетельствует о наличии касательных напряжений на их гранях, т.е. напряженное состояние в любой точке представляет собой чистый сдвиг.
(рис. 5.3). Прямоугольная сетка, нанесенная на его поверхности, после деформации превратится в сетку, состоящую из параллелограммов, что свидетельствует о наличии касательных напряжений на их гранях, т.е. напряженное состояние в любой точке представляет собой чистый сдвиг.
Примем следующие гипотезы: 1. Все поперечные сечения остаются плоскими и после деформации. 2. Радиусы поперечных сечений остаются прямыми и после деформации. 3. Расстояния между поперечными сечениями последеформации не изменяются. Вырежем двумя поперечными сечениями 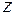 и
и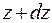 часть стержня и закрепим левым торцом (рис. 5.4).
часть стержня и закрепим левым торцом (рис. 5.4).
В элементе 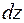 радиусом
радиусом 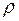 выделим цилиндрический cлой, образующая
выделим цилиндрический cлой, образующая 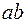 которого после деформации займет положение
которого после деформации займет положение 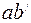 под воздействием крутящего момента
под воздействием крутящего момента 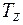 , который для элемента
, который для элемента 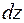 можно считать внешним крутящим моментом. Поперечные сечения повернутся взаимно на угол
можно считать внешним крутящим моментом. Поперечные сечения повернутся взаимно на угол 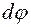 [рад].
[рад].
Из рис. 5.4 cледует: 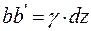 или
или 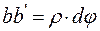 . Приравняв правые части, подучим:
. Приравняв правые части, подучим:
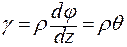 .
.
Обозначим
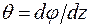 ,
,
где q - относительный угол закручивания [рад/м].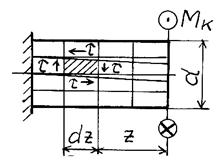
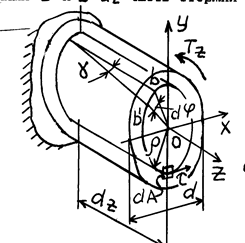 |
Рис. 5.3 Рис.5.4
Элемент 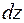 испытывает чистый сдвиг, следовательно справедлив закон Гука при сдвиге. Для слоя с радиусом
испытывает чистый сдвиг, следовательно справедлив закон Гука при сдвиге. Для слоя с радиусом 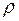 получим
получим 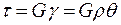 ,
,
т.е. касательные напряжения в сечении меняются по линейному закону.
Установим зависимость между крутящим моментом 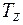 и касательными напряжениями в поперечном сечении:
и касательными напряжениями в поперечном сечении:
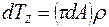
или: 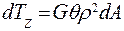 .
.
Откуда 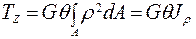 ,
,
где 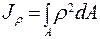 - полярный момент инерции.
- полярный момент инерции.
Получим формулу для определения относительного угла закручивания
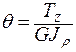 .
.
Подставив получим формулу для определения в любой точке поперечного сечения:
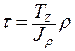 ,
,
где: 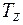 - крутящий момент в сечении, в котором определяют напряжения [Н·м];
- крутящий момент в сечении, в котором определяют напряжения [Н·м];
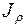 - полярный момент инерции поперечного сечения для круга [м4];
- полярный момент инерции поперечного сечения для круга [м4];
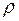 - радиус слоя поперечного сечения, в котором определяют напряжения.
- радиус слоя поперечного сечения, в котором определяют напряжения.
Таким образом, следует, что наибольшие напряжения возникают в точках контура поперечного сечения при 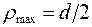 . Эпюра
. Эпюра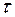 представлена на
представлена на
рис. 5.5, а. По формуле получим 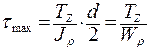 , где
, где 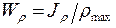 - полярный мо-
- полярный мо-
а) б) мент сопротивления поперечного
Рис. 5.5 сечения.
Для круга диаметра 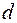 полярный момент сопротивления равен:
полярный момент сопротивления равен:
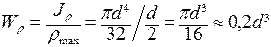 .
.
для кольца наружного диаметра 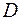 и внутреннего диаметра
и внутреннего диаметра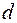 (рис. 5.5, б) получим:
(рис. 5.5, б) получим:
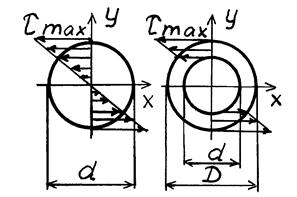
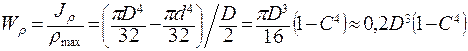 ,
,
где 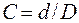 .
.
5.3. Расчёт на прочность при кручении. Наибольшие напряжения возникают в опасном сечении вала – сечении, в котором возникает наибольший по абсолютной величине внутренний крутящий момент
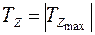 .
.
Условие прочности 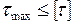 имеет вид
имеет вид
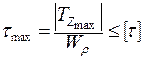 .
.
Допускаемое напряжение на кручение, как и при других видах деформации, определяют по формуле
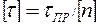 ,
,
где 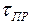 – предельное напряжение (
– предельное напряжение (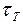 – для пластичных и
– для пластичных и 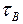 – для хрупких материалов), а
– для хрупких материалов), а 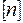 – коэффициент запаса прочности.
– коэффициент запаса прочности.
Т.к. данных испытания различных материалов на кручение значительно меньше, чем на растяжение, то 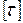 принимают из опыта по
принимают из опыта по 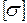 . Так, например, для стали
. Так, например, для стали 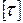
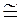 0,5
0,5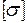 , для чугуна
, для чугуна 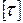
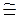
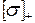 .
.
Также как и при растяжении и изгибе при расчёте на прочность при кручении возможны следующие три вида задач, различающихся формой использования условия прочности:
Проверочный расчёт – выполняется по формуле для опасного сечения вала.
Проектировочный расчет – подбор размеров сечения вала.
Для круга:
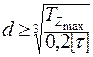 ;
;
для кольца имеют
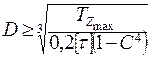 ,
,
где 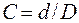 - заданное отношение диаметров.
- заданное отношение диаметров.
Определение допускаемой нагрузки. Тогда
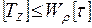 .
.
 2014-02-09
2014-02-09 2687
2687
