УНИВЕРСАЛЬНОЕ ОТОБРАЖЕНИЕ ПЕРЕМЕЖАЕМОСТИ
З.Ж. Жанабаев, С. Н. Ахтанов
Казахский национальный университет им. аль- Фараби, г. Алматы.
Из условия фрактальности меры получено универсальное отображение, описывающее ее перемежаемую эволюцию типа «накопление - выброс». В отличие от всех известных дифференциальных и дискретных моделей динамической системы данное отображение реализует хаотические колебания с характеристиками, соответствующими критериям самоорганизации.
Введение
Перемежаемость – чередование порядка и хаоса является универсальным явлением природы. Этот термин является общепринятым в гидродинамике и означает чередование ламинарного режима движения жидкости с турбулентным. Аналогичные картины наблюдаются во временном ряде астрофизических, сейсмических, нейрофизических, нанотехнологических и других процессов. При этом общей закономерностью является также нерегулярная смена мелкомасштабных флуктуаций с крупномасштабными. В моделях динамических систем перемежаемость тоже наблюдается универсальным образом, как правило, в виде смены процессов удвоения периода (например, через отображение Фейгенбаума) с хаосом.
Вышеперечисленные процессы с перемежаемостью реализуются в нелинейных, неравновесных и незамкнутых (открытых) системах, т.е. при наличии условий для самоорганизации. Процесс самоорганизации имеет самоподобные динамические характеристики, его фазовый портрет может быть странным (фрактальным) аттрактором. Отсюда следует естественный вопрос: можно ли записать в наиболее простом и универсальном виде уравнение (отображение) перемежаемых процессов с всплесками, имеющих фрактальные, синергетические закономерности? Поиск ответа на этот вопрос является целью настоящей работы.
Уравнение фрактальной эволюции и его дискретная форма
Эволюцию некоторой функции x(t), связанной с фрактальной мерой (аддитивной величины, характеризующейся измеримым множеством) по времени t запишем в виде
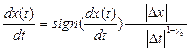 , (1.1)
, (1.1)
где 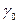 - статистическая характеристика множества значений t, она введена с целью обеспечения условия Лифшица – Гельдера для ограничения производной
- статистическая характеристика множества значений t, она введена с целью обеспечения условия Лифшица – Гельдера для ограничения производной 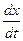 . Модуль приращения
. Модуль приращения 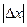 (масштаб измерения величины x(t)) заменим из условия фрактальности меры
(масштаб измерения величины x(t)) заменим из условия фрактальности меры  :
:
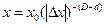 ,
, 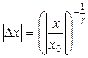 ,
, 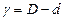 , (1.2)
, (1.2)
где 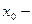 нефрактальная регулярная мера,
нефрактальная регулярная мера, 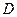 - фрактальная размерность множества значений
- фрактальная размерность множества значений  , d- топологическая размерность носителя меры.
, d- топологическая размерность носителя меры.
Подставив формулу (1.2) в формулу (1.1) перейдем к дискретным разностям. Можно убедиться, что в дискретном случае знаковая функция будет связана с плотностью вероятности 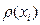 , где
, где 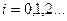 - номер шага по времени реализации
- номер шага по времени реализации 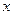 .
.
Воспользуемся законом сохранения вероятности
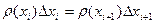 . (1.3)
. (1.3)
Принимая 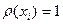 , имеем
, имеем
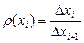 ,. (1.4)
,. (1.4)
Для определения плотности вероятности нужно воспользоваться модулем производной в (1.4), если в формуле (1.4) учесть знак производной, то мы автоматически получим искомую знаковую функцию sign(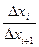 ).
).
С целью описания самоподобных свойств системы мы определяем производную в (1.4) в неподвижной точке 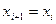 :
:
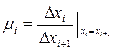 . (1.5)
. (1.5)
Это выражение в дифференциальной форме в теории динамического хаоса называется мультипликатором.
С учетом формул (1.2), (1.4), (1.5) формулу (1.1) для случая 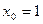 запишем в виде
запишем в виде
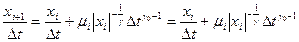 . (1.6)
. (1.6)
В формуле (1.6), чтобы можно было выбрать одинаковые моменты времени, исключим величину 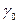 . Для этой цели выберем зависимость модуля
. Для этой цели выберем зависимость модуля 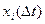 в виде обобщенного броуновского движения [1]
в виде обобщенного броуновского движения [1]
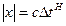 , (1.7)
, (1.7)
где 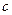 - коэффициент диффузии,
- коэффициент диффузии, 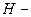 показатель Херста.
показатель Херста.
Запишем (1.6) в следующем виде:
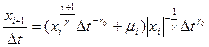 . (1.8)
. (1.8)
Примем обозначение 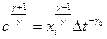 . Вид обозначения выбран так, чтобы удовлетворить стандартным условиям
. Вид обозначения выбран так, чтобы удовлетворить стандартным условиям
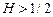 ,
, 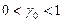 . (1.9)
. (1.9)
Из (1.9) имеем:
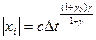 . (1.10)
. (1.10)
Сравнивая формулы (1.10), (1.7) получим:
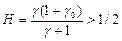 . (1.11)
. (1.11)
Отсюда следует, что всегда 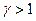 ,
, 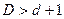 .
.
Принимая 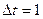 окончательно запишем уравнение (1.8) в следующем виде:
окончательно запишем уравнение (1.8) в следующем виде:
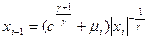 . (1.12)
. (1.12)
Продифференцировав (1.12) получим:
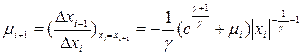 . (1.13)
. (1.13)
Формулы (1.12) и (1.13) представляют собой искомое отображение перемежаемости.
 2015-06-26
2015-06-26 247
247







