Эволюционный параметр порядка

Необходимо установить количественную характеристику сложных – перемежаемых, сильно неоднородных сигналов. Известная характеристика сложности сигнала - база определяется как:

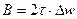, (2.1)

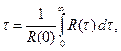
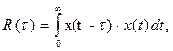
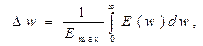(2.2) где 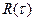- корреляционная функция, 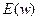- спектр мощности, 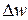— эффективная ширина полосы частот, 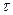— эффективное время корреляции.

Смысл использования выражения (2.1) в качестве меры неопределенности в волновых процессах соответствует тому, что существует минимальная ячейка фазового пространства (аналогия соотношения неопределенности в квантовой физике). Но корреляционная функция и соответствующий ей спектр мощности является энергетической характеристикой, они не учитывают информацию о фазе, форме колебаний. Искомую меру сложности нужно определить непосредственно через реализацию . Вначале мы рассмотрим чисто метрическую характеристику сложности, а соответствующую топологическую (информационно - энтропийную) характеристику обсудим отдельно.

Существование метрических характеристик (длины, площади, объема) следует из выполнения интегрального неравенства Гёльдера для любых функций , :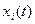

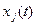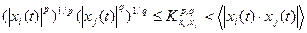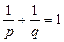, , (2.3)

где равенство выполняется при постоянном 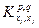. В физических приложениях можно пользоваться усреднением по времени 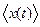. В случае 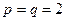искомая характеристика определяется на евклидовой поверхности с топологической размерностью 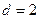. Если 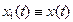, , 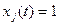, 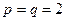то мы получим 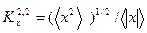- коэффициент формы сигнала, который используется в радиофизике.

Если принять 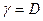, , 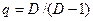то характеристику взаимной сложности можно определить на множестве с фрактальной размерностью 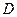. При этом возможное асимптотическое значения 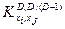можно найти итерационным путем: принять в качестве исходного значения фрактальной меры 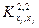, затем по формуле определения фрактальной размерности найти 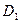(результат первого приближения) и использовать 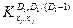и т.д.

Для случая равенства в формуле (2.3)

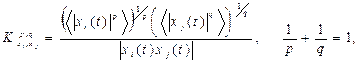(2.4)

мы получим минимальное значение меры сложности (неоднородности) выражения в правой части для двух произвольных функций. Формула (2.4) отличается от обратного коэффициента нецентрированной автокорреляции: усредняется модуль произведения функций, учитывается возможность .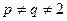

Перемежаемые функции являются сильно неоднородными относительно друг друга (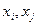) и относительно аргумента (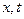). В терминах теории подобия, масштабной инвариантности перемежаемые сигналы не являются подобными, а афинными: не обладают свойством самоподобия, а могут быть самоаффинными. Чтобы учесть такую неравновесность в силу произвольности функций 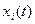, 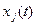в формуле (2.4) мы можем выбрать одну из них в качестве параметра порядка – определяющей переменной. Если нас интересует эволюция по времени 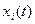, то можно выбрать 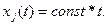Тогда выражение (2.4) при 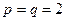имеет вид

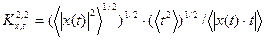. (2.5)

Для описания физических процессов представляет интерес выражение

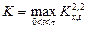, (2.6)

где 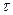- характерное время, при котором 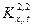достигает максимума.

Выражение (2.5) назовем эволюционным параметром порядка. Этот параметр имеет смысл безразмерного времени и является пропорциональным номеру шага дискретных отображений динамических систем.