В физике открытых систем важными являются вопросы, связанные с определением режимов самоподобия и самоаффинности. Если число определяющих переменных больше единицы и коэффициенты подобия по этим переменным различные, то фрактальный объект называется самоаффинным. Если иерархические части фрактального объекта имеют одинаковые коэффициенты подобия по всем переменным, то объект называется самоподобным. В работе З. Ж. Жанабаева [2] были установлены информационно – энтропийные критерии самоаффинности (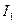 ) и самоподобия (
) и самоподобия (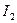 ) в виде неподвижных точек плотности вероятности реализации информации и энтропии:
) в виде неподвижных точек плотности вероятности реализации информации и энтропии:
 ,
, 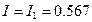 ;
; 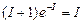 ,
, 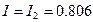 . (3.1)
. (3.1)
В последние годы развивается новая обобщенная статистическая механика, которую можно назвать статистикой Цаллиса, или, квазиканонической статистикой Гиббса [3]. В основе таких теорий лежит использование экспоненциальной функции вида
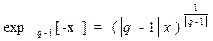 . (3.2)
. (3.2)
В пределе 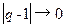 мы имеем обычную функцию
мы имеем обычную функцию 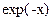 , которая описывает каноническое распределение Гиббса. Отличие от единицы параметра
, которая описывает каноническое распределение Гиббса. Отличие от единицы параметра 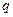 характеризует степень статистической неравновесности, неоднородности системы. Для простоты мы далее будем пользоваться выражением
характеризует степень статистической неравновесности, неоднородности системы. Для простоты мы далее будем пользоваться выражением 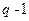 вместо
вместо 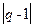 , при необходимости выбирая положительный знак искомой физической величины.
, при необходимости выбирая положительный знак искомой физической величины.
Используя выражение (3.2) мы определим зависимость от 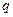 информационной энтропии – единственной меры сложности, неопределенности неравновесной системы. Для квазиравновесного процесса, характеризуемого параметром
информационной энтропии – единственной меры сложности, неопределенности неравновесной системы. Для квазиравновесного процесса, характеризуемого параметром 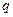 , информацию определим в виде
, информацию определим в виде
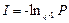 . (3.3)
. (3.3)
Отсюда представим вероятность как функцию от информации:
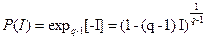 . (3.4)
. (3.4)
Функция плотности распределения вероятности реализации информации 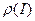 определяется как
определяется как
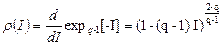 . (3.5)
. (3.5)
Энтропия определяется как среднее значение информации:
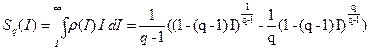 . (3.6)
. (3.6)
Самоподобные значения 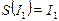 и
и 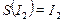 найдем как неподвижные точки отображений
найдем как неподвижные точки отображений
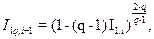 (3.7)
(3.7)
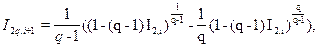 (3.8)
(3.8)
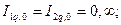
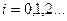 .
.
Таким образом, параметр 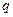 может характеризовать отклонение системы от состояния самоподобия и самоаффинности через значения информации и информационной энтропии. При условии
может характеризовать отклонение системы от состояния самоподобия и самоаффинности через значения информации и информационной энтропии. При условии
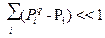 , (3.9)
, (3.9)
энтропия Цаллиса, определяемая формулой (3.2), совпадает с энтропией Реньи:
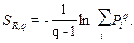 (3.10)
(3.10)
Параметр неоднородности можно определить по формуле [4]:
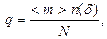 (3.11)
(3.11)
где 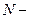 общее число точек (отсчетов),
общее число точек (отсчетов), 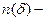 минимальное число ячеек с масштабом измерения
минимальное число ячеек с масштабом измерения  , покрывающих площадь
, покрывающих площадь 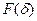 , ограниченной кривыми
, ограниченной кривыми 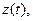
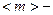 среднее число точек в ячейке. Для простоты можно принять
среднее число точек в ячейке. Для простоты можно принять 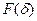 как фигуру, ограниченной прямыми, соединяющими локальные максимумы z(t) и
как фигуру, ограниченной прямыми, соединяющими локальные максимумы z(t) и 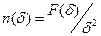 .
.
Параметр неоднородности также можно вычислить через отношение интеграла Римана к интегралу Лебега:
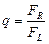 , (3.12)
, (3.12)
где 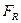 - интеграл от сигнала
- интеграл от сигнала  по
по 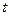 по Риману,
по Риману, 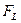 - интеграл Лебега.
- интеграл Лебега.
 Если исследуемый процесс представлен в виде произведении регулярной
Если исследуемый процесс представлен в виде произведении регулярной 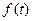 и случайной
и случайной 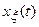 функций, тогда интеграл Римана запишется в виде:
функций, тогда интеграл Римана запишется в виде:
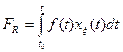 . (3.13)
. (3.13)
По методу Римана временная ось разбивается на равные промежутки 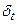 и в соответствии со значениями
и в соответствии со значениями 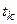 находятся значения функции, где
находятся значения функции, где 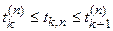 .
.
Если рассматриваемое явление носит случайный характер из-за множителя 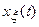 , то значения
, то значения 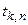 могут быть выбраны случайным образом (как в известном в литературе стохастическом интеграле Ито). В случае хаотических процессов необходимо выбрать точки
могут быть выбраны случайным образом (как в известном в литературе стохастическом интеграле Ито). В случае хаотических процессов необходимо выбрать точки 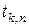 в соответствии со значениями функции, т.е.
в соответствии со значениями функции, т.е. 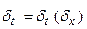 . Тогда интеграл (3.13) в виде меры Лебега запишется в виде
. Тогда интеграл (3.13) в виде меры Лебега запишется в виде
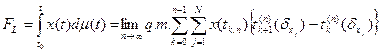 , (3.14)
, (3.14)
где 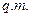 означает среднеквадратичный смысл суммы.
означает среднеквадратичный смысл суммы.
 2015-06-26
2015-06-26 300
300








